 Теорема 1 Теорема 1 |
|
Рассмотрим СЛАУ второго порядка: 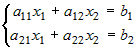 . Если . Если 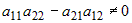 , то система имеет единственное решение, которое
определяется по формулам: , то система имеет единственное решение, которое
определяется по формулам: 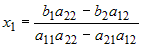 , , 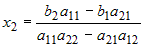 . . |
 Доказательство Доказательство |
|
Умножим первое уравнение системы на 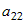 , а второе уравнение - на , а второе уравнение - на 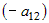 и сложим их. Получим линейное уравнение, в которое
входит только неизвестное и сложим их. Получим линейное уравнение, в которое
входит только неизвестное 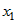 , , 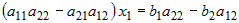 Если Если 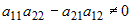 , то это уравнение имеет единственное решение: , то это уравнение имеет единственное решение: 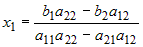 . .
Теперь умножим первое уравнение системы на 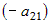 , а второе уравнение - на , а второе уравнение - на 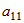 и сложим их. Получим линейное уравнение, в которое
входит только неизвестное и сложим их. Получим линейное уравнение, в которое
входит только неизвестное 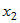 , , 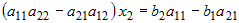 . Если . Если 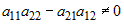 , то это уравнение имеет единственное решение: , то это уравнение имеет единственное решение: 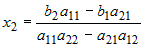 . . |
| Замечание
2 |
|
Обращаем Ваше внимание, что в
каждое слагаемое входит один и только один элемент из каждого столбца и
строки матрицы. |
Рассмотрим СЛАУ 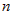 -ого порядка: -ого порядка: 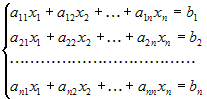 . Для нее так же справедливы формулы
Крамера. . Для нее так же справедливы формулы
Крамера. |
Замечание 3
Доказательство теоремы 4 будет
приведено далее.
|
 |