Введем в пространстве прямоугольную декартову систему координат 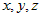 с началом в некоторой точке с началом в некоторой точке 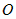 . Произвольную точку . Произвольную точку 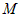 в этой системе координат будем задавать ее координатами в этой системе координат будем задавать ее координатами
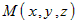 . Вектор . Вектор 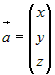 изображать направленным отрезком изображать направленным отрезком 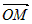 , начало которого может быть перенесено в
любую точку пространства (рис.1). , начало которого может быть перенесено в
любую точку пространства (рис.1).
 |
| Рис. 1 |
 |
Определение
1 |
|
Если в пространстве задана прямоугольная декартова
система координат, то алгебраическое уравнение 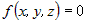 называется уравнением поверхности называется уравнением поверхности 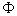 в этой системе координат,
если: в этой системе координат,
если: |
| 1. |
Координаты любой точки 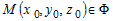 связаны уравнением связаны уравнением 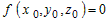 . . |
| 2. |
Для любого решения 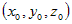 уравнения уравнения 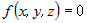 справедливо справедливо 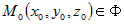 (рис. 2). (рис. 2).
 |
| Рис.
2 | |
Замечание
Иначе говоря, уравнение поверхности
связывает координаты тех и только тех точек, которые принадлежат этой
поверхности.
В дальнейшем будет дана классификация основных поверхностей, а в
данном разделе мы покажем, как получить уравнение поверхности, если задано общее
геометрическое свойство ее точек.
 |
Теорема
1 |
|---|
|
Линейное уравнение с тремя переменными 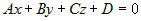 задает в пространстве
плоскость. задает в пространстве
плоскость. |
 |
Доказательство |
|---|
| 1. |
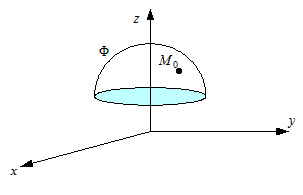
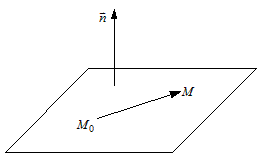
Пусть задана точка 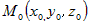 , принадлежащая плоскости, и вектор , принадлежащая плоскости, и вектор 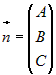 , перпендикулярный плоскости. Ясно,
что через данную точку перпендикулярно данному вектору можно провести
только одну плоскость (рис.3). , перпендикулярный плоскости. Ясно,
что через данную точку перпендикулярно данному вектору можно провести
только одну плоскость (рис.3).
 |
| Рис.
3 |
Если точка 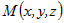 принадлежит искомой плоскости, то вектор принадлежит искомой плоскости, то вектор 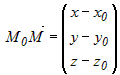 коллинеарен этой плоскости и ортогонален вектору коллинеарен этой плоскости и ортогонален вектору
 . Из ортогональности векторов следует . Из ортогональности векторов следует 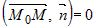 или или 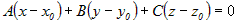 . Раскрывая скобки и обозначая . Раскрывая скобки и обозначая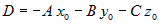 , получим уравнение , получим уравнение 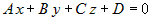 . Это линейное уравнение, причем коэффициенты при
переменных . Это линейное уравнение, причем коэффициенты при
переменных 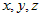 - координаты нормального вектора - координаты нормального вектора 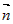 . .
|
| 2. |
Пусть 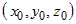 - какое-то решение
уравнения - какое-то решение
уравнения
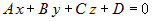 . (1) . (1) | Это
означает, что справедливо
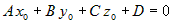 . (2) . (2) | Вычитая
из уравнения (1) уравнение (2), получим
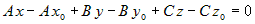 , или , или 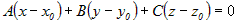 . .
Получили уравнение
плоскости, проходящей через точку 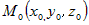 и перпендикулярной вектору и перпендикулярной вектору 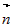 . . |
|
 |