 Общее уравнение кривой
второго порядка Общее уравнение кривой
второго порядка |
Если на плоскости задана прямоугольная декартова система
координат  , то кривая второго порядка
определяется уравнением второй степени , то кривая второго порядка
определяется уравнением второй степени |
  , , |
где  - заданные действительные числа. При этом числа - заданные действительные числа. При этом числа  одновременно не равны нулю. Уравнение (1) называется
общим уравнением кривой
второго порядка. Если нет точек одновременно не равны нулю. Уравнение (1) называется
общим уравнением кривой
второго порядка. Если нет точек  с действительными координатами, удовлетворяющих
уравнению с действительными координатами, удовлетворяющих
уравнению  , то говорят, что уравнение (1) определяет мнимую кривую
второго порядка. Уравнение , то говорят, что уравнение (1) определяет мнимую кривую
второго порядка. Уравнение  может служить примером
уравнения второй степени, определяющего мнимую кривую, в данном случае
мнимую окружность. может служить примером
уравнения второй степени, определяющего мнимую кривую, в данном случае
мнимую окружность. |
 Важные случаи общего
уравнения кривой второго порядка Важные случаи общего
уравнения кривой второго порядка |
| Уравнение эллипса |
  |
с полуосями длины  и и  . В частности, при . В частности, при  уравнение окружности уравнение окружности |
 |
с центром в начале координат и радиусом  . . |
| Уравнение гиперболы |
  |
с полуосями  и и  . . |
| Уравнение параболы |
  . . |
| Уравнение пары пересекающихся прямых |
 , ,  или или  . . |
| Уравнение пары параллельных или совпадающих
прямых |
  , или , или  . . |
 , ,  или или  . . |
| Уравнение, определяющее точку |
 , или , или  . . |
Эллипс
Эллипсом называется множество точек, сумма
расстояний от которых до двух заданных точек, называемых фокусами, есть
величина постоянная. |
 Теорема Теорема |
|
Если известны: расстояние между фокусами  и и  эллипса, равное эллипса, равное  и сумма расстояний от любой точки на эллипсе до
фокусов, равное и сумма расстояний от любой точки на эллипсе до
фокусов, равное  , то в прямоугольной декартовой системе координат, где ось , то в прямоугольной декартовой системе координат, где ось
 проходит через фокусы проходит через фокусы  и и  (от (от  к к  ), а начало координат посередине
между ними, уравнение эллипса имеет вид ), а начало координат посередине
между ними, уравнение эллипса имеет вид
 , где , где  . .
|
 Доказательство Доказательство |
|
 |
| Рис.
23 |
Во введенной системе координат фокусы расположены на оси  и имеют координаты и имеют координаты  и и  . Пусть точка . Пусть точка  принадлежит эллипсу (рис.23).
Тогда принадлежит эллипсу (рис.23).
Тогда
 , ,  , ,
 , ,
перенося первый радикал из правой части в левую,
запишем
 . .
Возведем обе части уравнения в квадрат

и раскроем квадраты в левой и правой частях
 . .
Приводя подобные члены, получим уравнение
 , ,
обе части которого разделим на  и снова возведем в квадрат.
тогда уравнение примет вид и снова возведем в квадрат.
тогда уравнение примет вид
 . .
Последнее уравнение можно упростить, если раскрыть
скобки и привести подобные члены,
 , ,
 . .
Поскольку из определения эллипса следует, что  , то число , то число  и его можно обозначить, как и его можно обозначить, как  . Тогда уравнение эллипса запишется в
виде . Тогда уравнение эллипса запишется в
виде
 , или , или  . .
Разделив последнее уравнение на  , получим , получим
 . .
Такое уравнение эллипса называется каноническим. |
 Исследование формы
кривой Исследование формы
кривой |
|
Если в уравнении эллипса  заменить заменить  на на  , то его вид не изменится. Это означает, что если
точка , то его вид не изменится. Это означает, что если
точка  принадлежит кривой, то точка принадлежит кривой, то точка  также принадлежит этой кривой. Следовательно, кривая
симметрична относительно оси ординат. Эллипс симметричен и
относительно оси абсцисс, потому что его уравнение не меняется при замене также принадлежит этой кривой. Следовательно, кривая
симметрична относительно оси ординат. Эллипс симметричен и
относительно оси абсцисс, потому что его уравнение не меняется при замене
 на на  . Учитывая это, достаточно изучить вид кривой в первой
четверти, то есть при условии . Учитывая это, достаточно изучить вид кривой в первой
четверти, то есть при условии  . .
При  можно задать кривую в виде явного уравнения можно задать кривую в виде явного уравнения  , ,  . Из этого уравнения ясно, что кривая проходит через точки . Из этого уравнения ясно, что кривая проходит через точки
 и и  . Эти точки называются вершинами эллипса. . Эти точки называются вершинами эллипса.
Эллипс - ограниченная кривая, которая находится внутри
прямоугольника  . Из явного уравнения эллипса ясно, что ордината . Из явного уравнения эллипса ясно, что ордината  при непрерывном возрастании при непрерывном возрастании  на отрезке на отрезке  монотонно убывает.
Следовательно, эллипс есть непрерывная замкнутая кривая, в первой четверти
она выпукла вверх, в любой ее точке можно провести касательную. В
остальных четвертях кривая строится с учетом симметрии относительно
координатных осей. монотонно убывает.
Следовательно, эллипс есть непрерывная замкнутая кривая, в первой четверти
она выпукла вверх, в любой ее точке можно провести касательную. В
остальных четвертях кривая строится с учетом симметрии относительно
координатных осей.
Числа  и и  называются полуосями эллипса. Поскольку называются полуосями эллипса. Поскольку  , то , то  и эллипс вытянут вдоль оси и эллипс вытянут вдоль оси  . При этом . При этом  называется большей полуосью, а называется большей полуосью, а  - меньшей полуосью эллипса. Вид кривой показан
на рисунке 24. - меньшей полуосью эллипса. Вид кривой показан
на рисунке 24.
 |
| Рис.
24. |
При  эллипс представляет собой окружность радиуса эллипс представляет собой окружность радиуса  с центром в начале координат.
Уравнение этой окружности с центром в начале координат.
Уравнение этой окружности
 . . |
Эксцентриситетом эллипса называется число  . Для эксцентриситета эллипса справедливо неравенство . Для эксцентриситета эллипса справедливо неравенство
 , поскольку из определения эллипса следует, что , поскольку из определения эллипса следует, что  . Эксцентриситет окружности . Эксцентриситет окружности  , поскольку для окружности , поскольку для окружности  и и  . .
Учитывая то, что эксцентриситет окружности  , можно сделать вывод, что чем больше
эксцентриситет эллипса, тем больше он вытянут относительно одной из осей
симметрии. , можно сделать вывод, что чем больше
эксцентриситет эллипса, тем больше он вытянут относительно одной из осей
симметрии. |
Гипербола
Гиперболой называется множество точек, разность
расстояний от которых до двух заданных точек, называемых фокусами, есть
величина постоянная. |
 Теорема Теорема |
|
Если известны: расстояние между фокусами  и и  гиперболы, равное гиперболы, равное  и разность расстояний от любой ее точки до фокусов,
равное и разность расстояний от любой ее точки до фокусов,
равное  , то в прямоугольной декартовой системе координат, где ось , то в прямоугольной декартовой системе координат, где ось
 проходит через фокусы проходит через фокусы  и и  (от (от  к к  ), а начало координат посередине между фокусами, уравнение
гиперболы имеет вид ), а начало координат посередине между фокусами, уравнение
гиперболы имеет вид  , где , где  и и  . . |
 Доказательство Доказательство |
 |
| Рис.
25. |
Во введенной системе  координаты фокусов равны координаты фокусов равны  , ,  . Если точка . Если точка  принадлежит гиперболе, то справедливо принадлежит гиперболе, то справедливо  , или , или  (рис.25). (рис.25).
Подставив в последнее равенство координаты точек  , получим , получим
 , ,
или  . .
Возведем обе части последнего уравнения в
квадрат

и упростим его, раскрыв все квадраты

и приведя подобные члены
 . .
Последнее уравнение разделим на  и снова возведем в квадрат и снова возведем в квадрат
 . .
Раскрыв скобки и сделав упрощения, получим
уравнение
 , ,
в котором  , поскольку , поскольку  из определения гиперболы. Из этого следует, что
можно ввести обозначение из определения гиперболы. Из этого следует, что
можно ввести обозначение  и записать уравнение гиперболы в виде и записать уравнение гиперболы в виде  . Разделив на . Разделив на  , получим уравнение гиперболы , получим уравнение гиперболы
 , ,
которое называется каноническим. |
 Исследование формы
кривой. Исследование формы
кривой. |
|
Из вида уравнения ясно, что гипербола симметрична относительно оси
 и оси и оси  . При . При  получим уравнение получим уравнение  , которое не имеет вещественных корней. Следовательно,
кривая не пересекает ось , которое не имеет вещественных корней. Следовательно,
кривая не пересекает ось  . При . При  получим уравнение получим уравнение  , корни которого , корни которого  . Следовательно, кривая пересекает ось . Следовательно, кривая пересекает ось  в точках в точках  и и  . Эти точки называются вершинами гиперболы. . Эти точки называются вершинами гиперболы.
Числа  и и  называются полуосями гиперболы, называются полуосями гиперболы,  - действительной полуосью, а - действительной полуосью, а  - мнимой полуосью. - мнимой полуосью.
Для части гиперболы, находящейся в первой
четверти, явное уравнение имеет вид
 , ,  , ,
из которого видно, что  принимает вещественные значения при принимает вещественные значения при  . Следовательно, нет точек кривой, расположенных в полосе . Следовательно, нет точек кривой, расположенных в полосе
 . Кроме того, из явного уравнения можно видеть, что при
возрастании . Кроме того, из явного уравнения можно видеть, что при
возрастании  на полуинтервале на полуинтервале  ордината ордината  возрастает и стремится к
бесконечности. возрастает и стремится к
бесконечности. |
 Определение Определение |
Прямая  является асимптотой кривой, заданной уравнением является асимптотой кривой, заданной уравнением  при при   , если , если |
 или или  . . |
 Теорема Теорема |
|
Прямые  являются асимптотами гиперболы. являются асимптотами гиперболы. |
 Доказательство Доказательство |
|
Для части гиперболы в первой четверти, определяемой равенством  и прямой и прямой  : :
  . .
Это означает, что прямая  является асимптотой гиперболы при является асимптотой гиперболы при  . В силу симметрии гиперболы относительно осей, так же как
и симметрии пары прямых . В силу симметрии гиперболы относительно осей, так же как
и симметрии пары прямых  относительно осей, можно сказать, что обе эти прямые
являются асимптотами как при относительно осей, можно сказать, что обе эти прямые
являются асимптотами как при  , так и при , так и при  . Вид кривой показан на рисунке 26. . Вид кривой показан на рисунке 26.
 |
| Рис. 26. |
Эксцентриситет гиперболы  , где , где  - действительная полуось. Так как у гиперболы - действительная полуось. Так как у гиперболы  , то ее эксцентриситет , то ее эксцентриситет  . .
Зависимость формы гиперболы от величины эксцентриситета можно выяснить,
если зафиксировать значение  и увеличивать значение параметра и увеличивать значение параметра  . При этом будут увеличиваться величина эксцентриситета . При этом будут увеличиваться величина эксцентриситета
 и значение параметра и значение параметра  , так как , так как  . но тогда будет расти и абсолютная величина . но тогда будет расти и абсолютная величина  углового коэффициента асимптот гиперболы.
Следовательно, при увеличении эксцентриситета увеличивается размах ветвей
гиперболы. углового коэффициента асимптот гиперболы.
Следовательно, при увеличении эксцентриситета увеличивается размах ветвей
гиперболы. |
Парабола
Параболой называется множество точек,
равноудаленных от некоторой точки, называемой фокусом, и прямой,
называемой директрисой. |
 Теорема Теорема |
|
Если точка  - фокус параболы, а прямая - фокус параболы, а прямая  - ее директриса и задано расстояние между ними, равное - ее директриса и задано расстояние между ними, равное
 , то в системе координат, где ось , то в системе координат, где ось  проходит через проходит через  перпендикулярно перпендикулярно  и направлена от фокуса к директрисе, а начало
координат выбрано посередине между ними, уравнение параболы имеет вид и направлена от фокуса к директрисе, а начало
координат выбрано посередине между ними, уравнение параболы имеет вид
 , ,  | |
 Доказательство Доказательство |
|
Во введенной системе координат координаты фокуса  и уравнение директрисы и уравнение директрисы  : :  (рис. 27). Если точка (рис. 27). Если точка  лежит на параболе, то справедливо лежит на параболе, то справедливо
 , или , или  , ,
где  - точка пересечения перпендикуляра, проведенного из - точка пересечения перпендикуляра, проведенного из
 на директрису на директрису  . .
 |
| Рис. 27 |
Поскольку
 и и  , то , то  , ,
что равносильно
 , или , или  , ,
откуда следует уравнение параболы
 , ,
которое называется каноническим. |
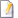 Задача 4 Задача 4 |
|
Построить кривую, заданную уравнением  . . |
 Решение Решение |
|
Разделив каждое слагаемое заданного уравнения на  , запишем его в виде , запишем его в виде  . Это уравнение задает на плоскости гиперболу с полуосями . Это уравнение задает на плоскости гиперболу с полуосями
 . Гипербола с равными полуосями называется
равнобочной, ее асимптотами являются биссектрисы координатных
углов . Гипербола с равными полуосями называется
равнобочной, ее асимптотами являются биссектрисы координатных
углов  . .
При  получим уравнение получим уравнение  , не имеющее вещественных корней, то есть гипербола не
пересекает ось , не имеющее вещественных корней, то есть гипербола не
пересекает ось  . При . При  , получим уравнение , получим уравнение  , имеющее корни , имеющее корни  . Следовательно, вершины гиперболы . Следовательно, вершины гиперболы  , ,  лежат на оси лежат на оси  . .
Фокусы гиперболы расположены на той же оси, на которой находятся ее
вершины. Из того, что  и и  , следует, что координаты фокусов , следует, что координаты фокусов  , ,  . Эксцентриситет гиперболы . Эксцентриситет гиперболы  . Вид кривой показан на рисунке 29. . Вид кривой показан на рисунке 29.
 |
| Рис. 29 | |
 Преобразование координат на плоскости. Преобразование координат на плоскости. |
|
Построение кривых заданных общим уравнением
Если сравнить канонические уравнения эллипса, окружности, гиперболы
и параболы с общим уравнением кривой второго порядка (1), то видно, что в
них коэффициенты  .
Если в этом уравнении .
Если в этом уравнении  , ,  или или  , то чтобы привести уравнение к каноническому виду,
определить тип кривой и построить ее, необходимо сделать преобразование
координат. , то чтобы привести уравнение к каноническому виду,
определить тип кривой и построить ее, необходимо сделать преобразование
координат.
Если в уравнении (1)  или или  , то это означает, что центр симметрии эллипса или
гиперболы, или центр окружности, или вершина параболы находятся не в
начале координат, а в некоторой точке , то это означает, что центр симметрии эллипса или
гиперболы, или центр окружности, или вершина параболы находятся не в
начале координат, а в некоторой точке  . Строить кривую в
данном случае удобно, перенося начало координат в эту точку, то есть,
сделав замену . Строить кривую в
данном случае удобно, перенося начало координат в эту точку, то есть,
сделав замену  . .
При такой замене в новой системе координат с началом в точке  и с осями и с осями  и и  уравнение кривой
будет иметь канонический вид. уравнение кривой
будет иметь канонический вид. |
 Уравнение эллипса с центром симметрии в точке Уравнение эллипса с центром симметрии в точке
 |
 . . |
 Уравнение гиперболы с центром симметрии в
точке Уравнение гиперболы с центром симметрии в
точке  |
 , , |
вершины в точках  и и  . . |
 , , |
вершины в точках  и и  . . |
 Уравнение параболы с вершиной в точке Уравнение параболы с вершиной в точке  |
 , , |
ось симметрии параллельна  . . |
 , , |
ось симметрии параллельна  . . |
Знак  показывает направление ветвей параболы. Если в
уравнении знак , то направление ветвей совпадает с направлением оси,
которой параллельна ось симметрии параболы. Если в уравнении знак -, то
направление ветвей противоположно направлению оси, которой параллельна ось
симметрии параболы. показывает направление ветвей параболы. Если в
уравнении знак , то направление ветвей совпадает с направлением оси,
которой параллельна ось симметрии параболы. Если в уравнении знак -, то
направление ветвей противоположно направлению оси, которой параллельна ось
симметрии параболы. |
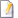 Задача Задача |
|
Построить кривую, заданную уравнением  , приведя его к
каноническому виду. , приведя его к
каноническому виду. |
 Решение Решение |
|
Преобразуем уравнение следующим образом
 , ,
 , ,
 , ,
 . .
Получили уравнение параболы с вершиной в точке  и с осью
симметрии, параллельной оси и с осью
симметрии, параллельной оси  . Перенося начало координат в точку . Перенося начало координат в точку  , получим в системе
координат , получим в системе
координат  уравнение уравнение
 , ,
где параметр  определяется из условия определяется из условия  или или  . .
Парабола симметрична относительно оси  или относительно
прямой или относительно
прямой  . Фокус
параболы находится на ее оси и отстоит от вершины на . Фокус
параболы находится на ее оси и отстоит от вершины на  . Поскольку из уравнения
следует, что . Поскольку из уравнения
следует, что  , то
ветви параболы направлены вниз и фокус , то
ветви параболы направлены вниз и фокус  лежит на лежит на  ниже вершины, то
есть его координаты ниже вершины, то
есть его координаты  . .
Директрисой параболы является прямая, перпендикулярная ее оси и
находящаяся на расстоянии  от вершины, причем фокус и директриса расположены по
разные стороны от вершины. Учитывая все это, можно записать уравнение
директрисы от вершины, причем фокус и директриса расположены по
разные стороны от вершины. Учитывая все это, можно записать уравнение
директрисы  , или , или
 . Кривая построена
на рис. 30. . Кривая построена
на рис. 30.
 |
| Рис.
30 | |
|
 |