 Теорема 2. (Предельный переход в
неравенстве). Теорема 2. (Предельный переход в
неравенстве). |
|
Если в некоторой окрестности точки 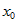 выполняется
неравенство выполняется
неравенство 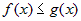 и
существуют конечные пределы и
существуют конечные пределы 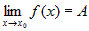 и и 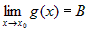 , то , то 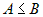 . . |
 Доказательство. Доказательство. |
|
Пусть 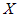 - общая область определения функций - общая область определения функций
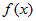 и и 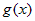 . Тогда по
определению предела функции . Тогда по
определению предела функции
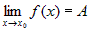  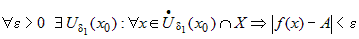 , ,
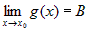   . .
Если в обоих случаях взять одно и то же 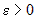 и из найденных
окрестностей и из найденных
окрестностей 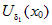 и и 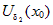 выбрать наименьшую, т. е. выбрать наименьшую, т. е. 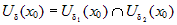 , то для , то для 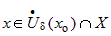 выполняются оба
неравенства одновременно, т. е. выполняются оба
неравенства одновременно, т. е.
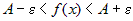 , , 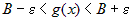 . .
Выберем 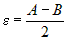 ,
предположив противное, т. е. пусть ,
предположив противное, т. е. пусть 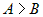 . Тогда . Тогда
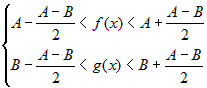 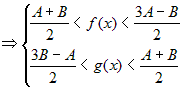 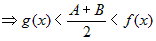 , ,
из последнего неравенства следует, что 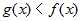 , что противоречит
условию теоремы, значит наше предположение , что противоречит
условию теоремы, значит наше предположение 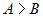 неверно.
Тогда верным является неравенство неверно.
Тогда верным является неравенство 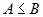 . . |
|
 |