Пусть функция 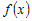 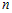 раз дифференцируема в некоторой окрестности раз дифференцируема в некоторой окрестности 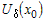 точки точки 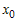 и пусть и пусть 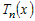 - ее многочлен Тейлора в точке - ее многочлен Тейлора в точке 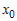 . Если обозначить . Если обозначить 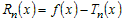 , то функцию , то функцию 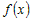 в окрестности в окрестности 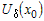 точки точки 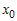 можно представить формулой: можно представить формулой:
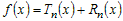 (1) (1) |
или
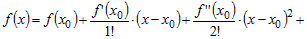
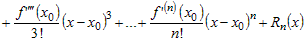 . (2) . (2) |
 Теорема Теорема |
|
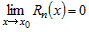
|
 Доказательство Доказательство |
|
очевидно, так как 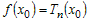 , а функция , а функция 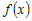 также, как и ее многочлен
Тейлора непрерывны. Тогда также, как и ее многочлен
Тейлора непрерывны. Тогда
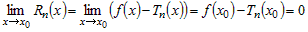 . .
| | Замечание |
Можно доказать, что остаточный член 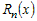 при при 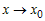 является бесконечно малой более высокого порядка,
чем является бесконечно малой более высокого порядка,
чем 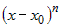 . Это записывается в следующем
виде: . Это записывается в следующем
виде:
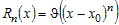 . .
Подобная форма записи остаточного члена формулы Тейлора называется
остаточным членом в форме Пеано.
Используя форму Пеано для остаточного члена, можно
записать формулу Тейлора в следующем виде.
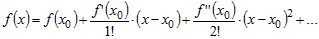
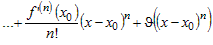 . .
|
 Определение 2 Определение 2 |
|
Пусть функция 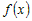 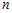 раз дифференцируема в некоторой окрестности раз дифференцируема в некоторой окрестности 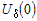 точки точки 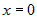 . Формула . Формула
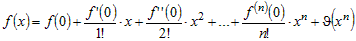 , ,
называется формулой Маклорена. |
| Замечание
1 |
|
Из определения ясно, что формула Маклорена получится из формулы
Тейлора, если положить 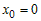 . . |
| Замечание
2 |
|
Можно доказать, что остаточный член формулы
Тейлора имеет вид:
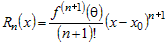 , ,
где 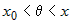 . Такая форма записи остаточного члена называется
остаточным членом в форме
Лагранжа. . Такая форма записи остаточного члена называется
остаточным членом в форме
Лагранжа. |
|
 |