Если 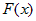 - первообразная для - первообразная для 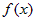 , то из равенства (1)
следует, что если , то из равенства (1)
следует, что если 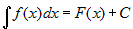 , то , то 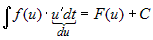 . .
Отсюда 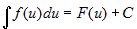 . На основании этого свойства получаем обобщенную таблицу
простейших интегралов, заменяя формально . На основании этого свойства получаем обобщенную таблицу
простейших интегралов, заменяя формально 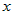 на на 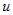 , где , где 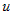 - любая непрерывно
дифференцируемая функция от независимой переменной, т. е. - любая непрерывно
дифференцируемая функция от независимой переменной, т. е. 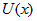 . Так, например, . Так, например,
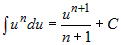 , где , где 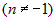 или или 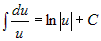 и
т.д. и
т.д. |
Отметим ряд преобразований дифференциала, полезных для дальнейшего:
 |
Отметим ряд
преобразований дифференциала, полезных для дальнейшего: |
| 1) |
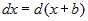 , где , где
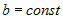 ; ; |
| 2) |
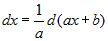 , где , где
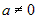 ; ; |
| 3) |
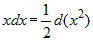 ; ; |
| 4) |
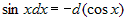 ; ; |
| 5) |
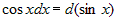 ; ; |
| 6) |
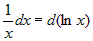 ; ; |
| 7) |
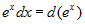 и
т.д. и
т.д. |
Вообще, 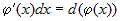 . Пользуясь этими преобразованиями дифференциала, найдем
следующие неопределенные интегралы. . Пользуясь этими преобразованиями дифференциала, найдем
следующие неопределенные интегралы.
Сформулируем еще одно очень полезное правило:
если 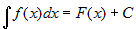 , то , то 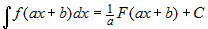 , ,
где 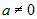 , так как , так как 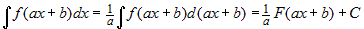 . . |
 Пример. Пример. |
|
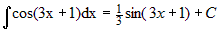 . .
|
|
 |