|
1) Пусть функция 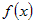 - дифференцируема в точке - дифференцируема в точке 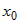 . Тогда по определению
дифференцируемой функции ее приращение можно представить в виде . Тогда по определению
дифференцируемой функции ее приращение можно представить в виде 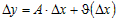 , где , где 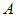 - конечное число, а - конечное число, а 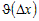 - бесконечно малая при - бесконечно малая при 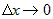 функция более высокого порядка, чем функция более высокого порядка, чем 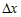 . .
Разделив это равенство на 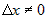 и перейдя к пределу при и перейдя к пределу при 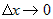 , получим , получим
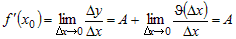 . .
Следовательно, производная 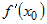 существует и равна конечному числу существует и равна конечному числу 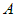 . .
2) Пусть в точке 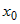 существует конечная производная существует конечная производная 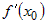 . Это означает, что существует и
равен конечному числу предел . Это означает, что существует и
равен конечному числу предел 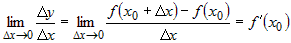 . .
Обозначим 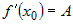 и воспользуемся тем, что
разность между функцией и ее конечным пределом является бесконечно малой в
точке, в которой вычисляется этот предел. Тогда и воспользуемся тем, что
разность между функцией и ее конечным пределом является бесконечно малой в
точке, в которой вычисляется этот предел. Тогда
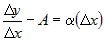 , где , где 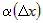 - бесконечно малая при - бесконечно малая при 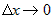 . .
Решая последнее равенство относительно приращения 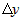 , получим , получим
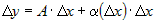 . .
Так как 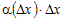 является бесконечно малой более высокого порядка, чем является бесконечно малой более высокого порядка, чем 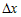 и можно обозначить и можно обозначить 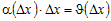 , то из полученного соотношения следует дифференцируемость
функции , то из полученного соотношения следует дифференцируемость
функции 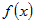 в точке в точке 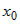 . . |