Пусть 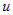 и и 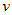 - непрерывно дифференцируемые функции от - непрерывно дифференцируемые функции от 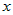 . На основании формулы дифференциала произведения
имеем: . На основании формулы дифференциала произведения
имеем:
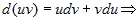 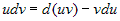
Интегрируя это соотношение, получим 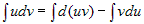 . .
Тогда 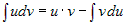 - формула интегрирования по частям. - формула интегрирования по частям.
Выведенная формула показывает, что 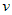 приводится к интегралу приводится к интегралу 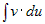 , который может оказаться более
простым, чем исходный. , который может оказаться более
простым, чем исходный. |
 |
Интегралы,
берущиеся "по частям" |
| 1. |
Интегралы вида 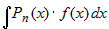 , где , где 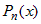 - многочлен степени - многочлен степени 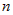 , , 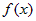 - одна из следующих функций: - одна из следующих функций: 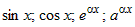 . . |
|
В качестве функции 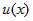 следует взять многочлен следует взять многочлен 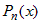 и применить к интегралу формулу интегрирования по
частям и применить к интегралу формулу интегрирования по
частям 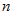 раз. раз.
|
| 2. |
Интегралы вида 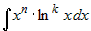 , где , где 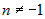 , берутся, если за функцию , берутся, если за функцию 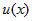 принять принять  и применить и применить 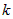 раз к интегралу формулу
интегрирования по частям. раз к интегралу формулу
интегрирования по частям. |
|
|
| 3. |
Интегралы вида 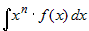 , где , где 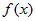 - одна из следующих функций: - одна из следующих функций: 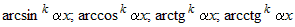 , также берутся "по частям", приняв за , также берутся "по частям", приняв за 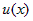 функцию функцию 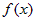 . . |
| 4. |
В некоторых случаях для сведения данного интеграла к
табличному применяется формула интегрирования по частям и искомый интеграл
определяется из получившегося алгебраического уравнения. К таким
интегралам относятся 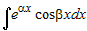 , , 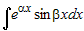 и и 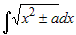 . . |
|
 Пример. Пример. |
|
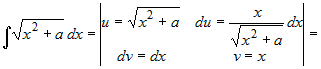
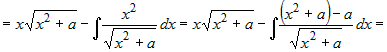
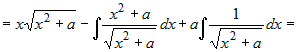
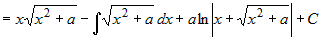 . .
Сравнивая начало и конец равенства, получим уравнение
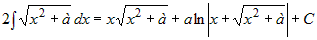 , откуда , откуда
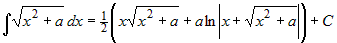 . .
| |
|
 |