Пусть на отрезке  задана непрерывная функция задана непрерывная функция 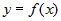 (рис. 1). Разделим (рис. 1). Разделим 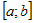 на части произвольными точками: на части произвольными точками: 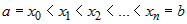 . Обозначим через . Обозначим через 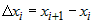 . . |
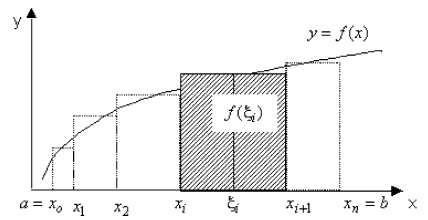 |
| Рис. 1 |
На каждом частичном отрезке 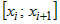 разбиения выберем произвольную точку разбиения выберем произвольную точку 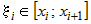 .В каждой точке .В каждой точке 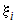 вычислим значение функции вычислим значение функции 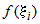 . .
Составим сумму 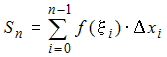 , которую будем называть интегральной
суммой функции , которую будем называть интегральной
суммой функции 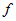 , соответствующей этому разбиению. , соответствующей этому разбиению.
Обозначим через 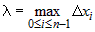 максимальную длину частичных отрезков максимальную длину частичных отрезков 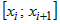 . . |
| Замечание |
|
Понятие определенного интеграла так, как мы его определили, было
введено для непрерывных функций французским математиком Коши. Говорят, что
непрерывная на отрезке 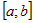 функция интегрируема на нем в смысле Коши. функция интегрируема на нем в смысле Коши.
В общем случае - для функций не обязательно непрерывных
- может существовать предел интегральных сумм, тогда говорят, что
функция интегрируема в смысле Римана. Это определение дано немецким
математиком Б. Ф. Риманом
(1826-1866гг.). |
|
 |