|
Выберем на прямой точку с аппликатой 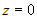 . Подставим . Подставим 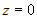 в общие уравнения прямой и найдем остальные
координаты точки из системы. в общие уравнения прямой и найдем остальные
координаты точки из системы. 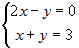 . Складывая уравнения системы, получим . Складывая уравнения системы, получим 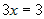 , или , или 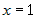 . Подставляя это в любое уравнение, найдем . Подставляя это в любое уравнение, найдем 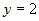 , Итак, точка , Итак, точка 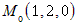 принадлежит прямой. Нормальные векторы плоскостей,
задающих прямую: принадлежит прямой. Нормальные векторы плоскостей,
задающих прямую: 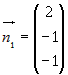 и и 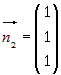 . Тогда направляющий вектор прямой равен их векторному
произведению . Тогда направляющий вектор прямой равен их векторному
произведению
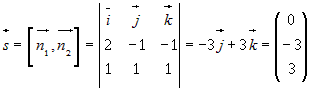 . .
Следовательно, канонические уравнения прямой имеют вид 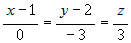 . . |