 Задача Задача |
|
Напишите уравнение плоскости, проходящей через точку 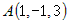 и отсекающей на координатных осях отрезки, равной
длины. и отсекающей на координатных осях отрезки, равной
длины. |
 Решение Решение |
|
Уравнение плоскости будем искать в виде 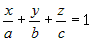 . Из условия . Из условия 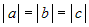 возможны следующие случаи: возможны следующие случаи:
1. 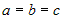 , тогда имеем , тогда имеем 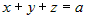 и, подставив в это уравнение координаты точки и, подставив в это уравнение координаты точки 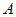 , найдем , найдем 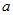 : : 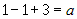 , или , или 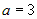 ; тогда уравнение плоскости запишется ; тогда уравнение плоскости запишется 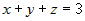 . .
2. 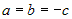 , тогда , тогда 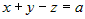 и для и для 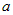 получим получим 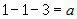 , или , или 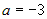 ; уравнение плоскости примет вид ; уравнение плоскости примет вид 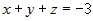 . .
3. 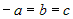 , , 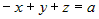 ; подставляем в это уравнение координаты точки ; подставляем в это уравнение координаты точки 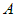 : : 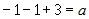 , или , или 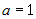 ; тогда уравнение плоскости ; тогда уравнение плоскости 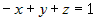 . .
4. 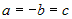 , , 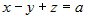 , , 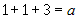 , или , или 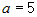 ; тогда уравнение плоскости запишется в виде ; тогда уравнение плоскости запишется в виде 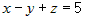 . . |
 Ответ: Ответ: |
|
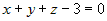 , или , или 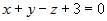 , или , или 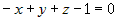 , или , или 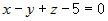 . .
|
|
 |