| Основными задачами, использующими скалярное произведение,
являются: |
 2. Вычисление проекции вектора на направление
другого вектора. 2. Вычисление проекции вектора на направление
другого вектора. |
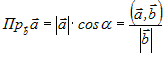 . . |
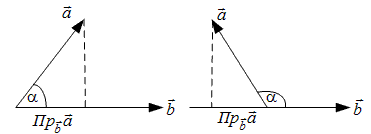 |
| Рис. 9 | |
 3. Вычисление работы, производимой вектором
силы по перемещению материальной точки. 3. Вычисление работы, производимой вектором
силы по перемещению материальной точки. |
Пусть под действием вектора силы 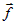 материальная точка материальная точка 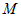 переходит в положение переходит в положение 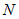 . Если ввести вектор перемещения . Если ввести вектор перемещения 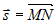 , то работу , то работу 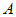 , производимую силой , производимую силой 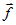 , можно вычислить следующим образом: , можно вычислить следующим образом: |
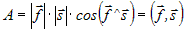 , (рис. 10) , (рис. 10) |
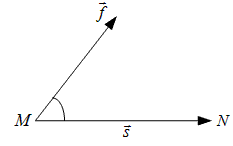 |
| Рис. 10 | |
|
 |