| Замечание
1 |
|
Если функция убывает или возрастает на всем промежутке 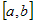 , то она называется монотонной (строго
монотонной) на промежутке , то она называется монотонной (строго
монотонной) на промежутке 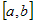 . . |
| Замечание
2 |
|
В определении 1 и 2 знаки неравенства между
значениями функции могут быть нестрогими. При этом:
если при 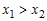 справедливо справедливо 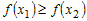 , то функция , то функция 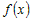 называется не убывающей (не строго возрастающей); называется не убывающей (не строго возрастающей);
если при 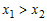 справедливо справедливо 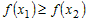 , то функция , то функция 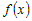 называется не
возрастающей (не строго убывающей). называется не
возрастающей (не строго убывающей). |
 Теорема 1 Теорема 1 |
|
Пусть функция 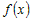 дифференцируема на промежутке дифференцируема на промежутке 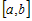 , если: , если:
· производная 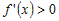 для всех значений для всех значений 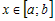 , то функция , то функция 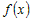 возрастает на промежутке возрастает на промежутке 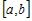 ; ;
· производная 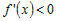 для всех значений для всех значений 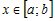 , то функция , то функция 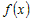 убывает на промежутке убывает на промежутке 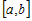 . . |
 Доказательство Доказательство |
|
Если 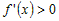 , то по определению производной в точке , то по определению производной в точке 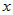 справедливо неравенство справедливо неравенство
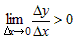 , или , или 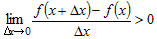 . .
Очевидно, что из этого следует неравенство
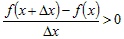 . (1) . (1)
В справедливости последнего неравенства легко убедиться, если
предположить обратное, то есть 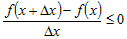 и перейти к пределу при и перейти к пределу при 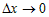 . Полученный результат . Полученный результат 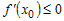 противоречит условию и
доказывает верность неравенства (1). Из неравенства (1) следует: противоречит условию и
доказывает верность неравенства (1). Из неравенства (1) следует:
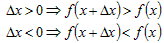 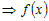 возрастает. возрастает.
Поскольку это выполняется во всех точках 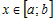 , то функция возрастает на всем промежутке , то функция возрастает на всем промежутке 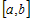 . .
Аналогично доказывается теорема для убывающей функции 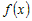 . . |
| Замечание
3 |
|
Если 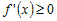 для всех, то для всех, то 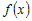 - не убывающая функция на промежутке - не убывающая функция на промежутке 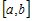 . Если . Если 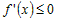 для всех для всех 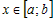 , то , то 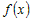 - не возрастающая функция на промежутке - не возрастающая функция на промежутке 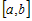 . . |
 Теорема 2 Теорема 2 |
|
Пусть функция 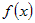 дифференцируема во всех точках
промежутка дифференцируема во всех точках
промежутка 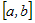 . .
· Если 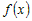 возрастает на промежутке возрастает на промежутке 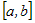 , то , то 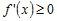 для всех значений для всех значений 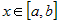 . .
· Если 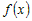 убывает на промежутке убывает на промежутке 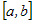 , то , то 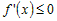 для всех значений для всех значений 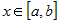 . . |
 Доказательство Доказательство |
|
Пусть функция 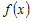 возрастает на промежутке возрастает на промежутке 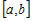 . Из определения возрастающей функции следует, что при . Из определения возрастающей функции следует, что при
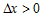 выполняется неравенство выполняется неравенство 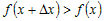 , которое равносильно неравенству , которое равносильно неравенству 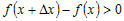 . .
Если 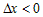 , то для возрастающей функции выполняется неравенство , то для возрастающей функции выполняется неравенство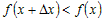 , или равносильное ему неравенство , или равносильное ему неравенство 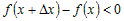 . .
Следовательно, выражения 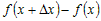 и и 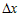 имеют одинаковые знаки, из чего
следует, что имеют одинаковые знаки, из чего
следует, что
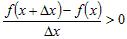 . .
Переходя в последнем неравенстве к пределу при 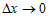 , получим, что , получим, что
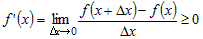 . .
Аналогично доказывается теорема для убывающей функции 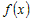 . . |
| Замечание
1 |
|
Аналогично доказывается теорема 2, если функция 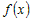 возрастает или убывает на промежутке возрастает или убывает на промежутке 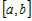 не строго. не строго. |
| Замечание
2 |
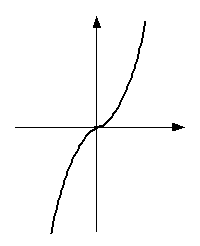 |
| Рис. 5 |
Следует иметь в виду, что производная строго возрастающей или строго
убывающей на промежутке  функции может в каких-то точках обращаться в ноль.
Примером является функция функции может в каких-то точках обращаться в ноль.
Примером является функция 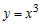 , которая строго возрастает на всей числовой оси (рис.5),
но ее производная , которая строго возрастает на всей числовой оси (рис.5),
но ее производная 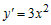 обращается в ноль при обращается в ноль при 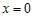 . .
|
|
 |