 Теорема Лагранжа. Теорема Лагранжа. |
Если функция 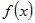 : : |
· непрерывна на 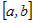 ; ; |
· дифференцируема на 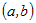 , , |
то существует точка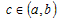 , для которой выполняется условие , для которой выполняется условие 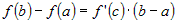 . . |
 Доказательство Доказательство |
|
Чтобы доказать эту теорему, построим функцию 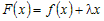 и подберем число и подберем число 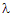 так, чтобы эта функция
удовлетворяла условиям теоремы Ролля. так, чтобы эта функция
удовлетворяла условиям теоремы Ролля.
Первые два условия выполнены, что ясно из вида функции. Чтобы было
верным третье условие число 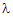 должно определяться из соотношения должно определяться из соотношения 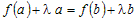 , из которого следует, что , из которого следует, что 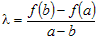 . .
Тогда для функции 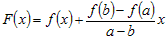 , удовлетворяющей всем условиям теоремы Ролля, найдется
точка , удовлетворяющей всем условиям теоремы Ролля, найдется
точка 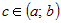 , такая, что , такая, что 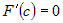 . Поскольку . Поскольку 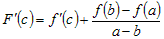 , то , то 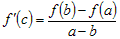 , или , или 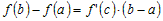 . .
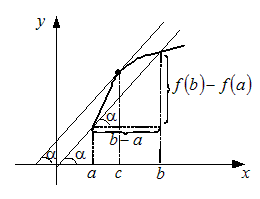 |
| Рис.10. |
Геометрический смысл теоремы Лагранжа состоит в том, что для
непрерывной на промежутке 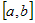 и дифференцируемой, по крайней мере, во внутренних
его точках функции всегда найдется точка и дифференцируемой, по крайней мере, во внутренних
его точках функции всегда найдется точка 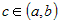 , касательная в которой параллельна прямой, соединяющей
точки графика функции с абсциссами , касательная в которой параллельна прямой, соединяющей
точки графика функции с абсциссами 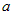 и и 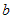 (рис.10). (рис.10).
Из рисунка 10 ясно, что 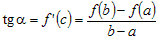 , откуда следует , откуда следует 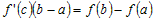 . . |
 Правило Лопиталя Правило Лопиталя |
|
Если функции 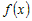 и и 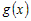 - дифференцируемы в окрестности - дифференцируемы в окрестности 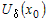 точки точки 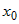 и если выполняется условие и если выполняется условие 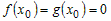 , причем , причем 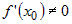 или или 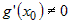 , то существует предел , то существует предел 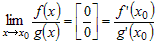 . . |
 Доказательство Доказательство |
|
Поскольку 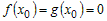 , то отношение , то отношение 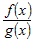 можно представить в виде можно представить в виде 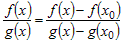 . .
Обе функции 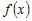 и и 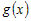 удовлетворяют условиям теоремы Лагранжа в
окрестности удовлетворяют условиям теоремы Лагранжа в
окрестности 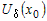 . Тогда по теореме Лагранжа найдутся точка . Тогда по теореме Лагранжа найдутся точка 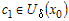 и точка и точка 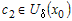 , такие, что для всех значений , такие, что для всех значений 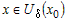 справедливо справедливо
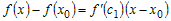 , ,
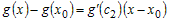 . .
Тогда выражение под знаком предела можно представить в виде
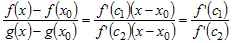 , ,
откуда следует, что 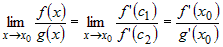 , так как при , так как при 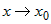 выполняются условия выполняются условия 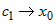 и и 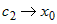 . . |
| Замечание 1 |
|
Можно доказать правило Лопиталя в общем виде
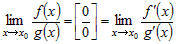 . .
Это замечание позволяет применять правило Лопиталя несколько раз, то
есть для дважды дифференцируемых в окрестности 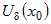 функций функций 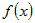 и и 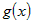 предел их отношения равен предел их отношения равен
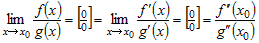 , ,
в том случае, когда 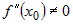 или или 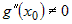 . .
Если же 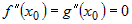 , а функции , а функции 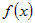 и и 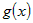 - трижды дифференцируемы в окрестности - трижды дифференцируемы в окрестности 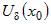 , то правило применяется еще раз, и так далее, до тех пор,
пока не устранится неопределенность. , то правило применяется еще раз, и так далее, до тех пор,
пока не устранится неопределенность. |
 Пример 1 Пример 1 |
|
Вычислить предел, используя правило Лопиталя 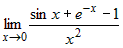 . . |
 Решение Решение |
|
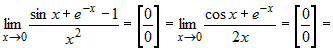
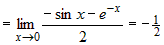 . .
|
| Замечание 2 |
|
Правило Лопиталя справедливо и в том случае, когда 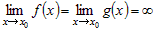 . . |
 Пример 2 Пример 2 |
|
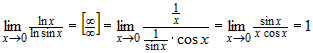 . .
|
 Пример 3 Пример 3 |
|
Вычислить предел, используя правило Лопиталя 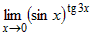 . . |
 Решение Решение |
|
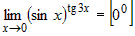 . Такой
вид неопределенности раскрывается с помощью основного логарифмического
тождества. Представим сложно-показательную функцию под знаком предела в
виде: . Такой
вид неопределенности раскрывается с помощью основного логарифмического
тождества. Представим сложно-показательную функцию под знаком предела в
виде:
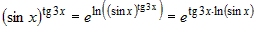 . .
Затем вычислим предел показателя
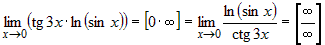 . .
Применяя правило Лопиталя, получим
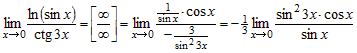 . .
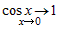 , а
бесконечно малые при , а
бесконечно малые при 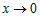 функции функции 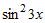 и и 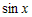 можно заменить под знаком предела эквивалентными
бесконечно малыми функциями можно заменить под знаком предела эквивалентными
бесконечно малыми функциями 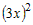 и и 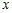 . Учитывая это, получим . Учитывая это, получим
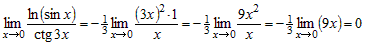 . .
Тогда 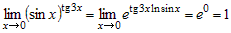 . . |
|
 |