|
Представим функцию в окрестности точки 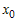 формулой Тейлора: формулой Тейлора:
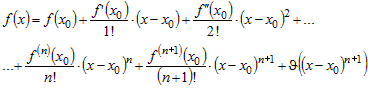 . .
Так как 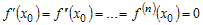 , то формула примет вид , то формула примет вид
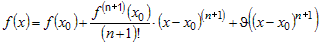 . .
Учитывая это и используя форму Лагранжа для записи остаточного члена,
получим
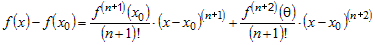 , ,
где 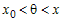 . Проведем некоторые упрощения . Проведем некоторые упрощения
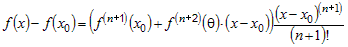 (1) (1)
и сделаем замену
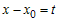 , , 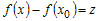 , ,
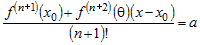 . .
Ясно, что в достаточно малой окрестности 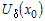 знак знак 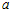 определяется знаком производной определяется знаком производной 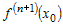 . Учитывая сделанную замену, равенство (1) перепишем в
переменных . Учитывая сделанную замену, равенство (1) перепишем в
переменных 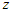 и и 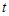 . .
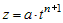 . .
В достаточно малой окрестности 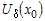 исследуемая функция ведет себя так же, как и
степенная функция исследуемая функция ведет себя так же, как и
степенная функция 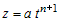 в окрестности точки в окрестности точки 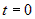 . В зависимости от четности показателя степени . В зависимости от четности показателя степени 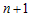 и от знака коэффициента и от знака коэффициента 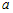 (рис.30), можно сделать вывод: (рис.30), можно сделать вывод:
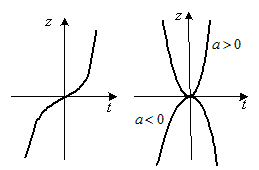 |
| Рис. 30
a Рис.
30 b. |
- если число 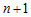 - нечетное, то в точке - нечетное, то в точке 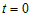 перегиб (рис.30 a); перегиб (рис.30 a);
- если число 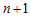 - четное, то в точке - четное, то в точке 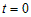 экстремум; максимум при экстремум; максимум при 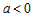 и минимум при и минимум при 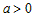 (рис.30 b). (рис.30 b). |