Замечание 1.
Заметим, что согласно определению полное
приращение 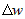 дифференцируемой функции представимо в виде двух частей.
Первая часть - 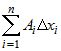 является линейной относительно приращений 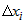 . а вторая - 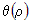 является бесконечно малой более высокого порядка, чем
каждое приращение 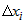 .
Замечание 2.
В отличие от функции одной переменной
для функции многих переменных нельзя дать условие, которое является одновременно
необходимым и достаточным условием дифференцируемости.
 Теорема 1. (Необходимое
условие дифференцируемости). Теорема 1. (Необходимое
условие дифференцируемости). |
Если функция 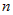 переменных дифференцируема в
некоторой точке, то она непрерывна в этой точке и имеет в ней конечные
частные производные по всем переменным. переменных дифференцируема в
некоторой точке, то она непрерывна в этой точке и имеет в ней конечные
частные производные по всем переменным. |
 Доказательство. Доказательство. |
Пусть функция 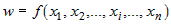 дифференцируема в точке дифференцируема в точке 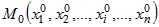 из области определения из области определения 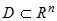 . По определению ее полное приращение . По определению ее полное приращение 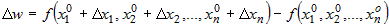 можно представить в виде: можно представить в виде: |
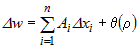 (1) (1) |
| Из этого следует: |
1) Приращения 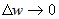 при всех при всех 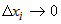 , , 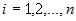 . Это ясно из того, что . Это ясно из того, что 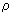 - бесконечно малая при - бесконечно малая при 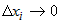 , , 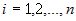 , а поскольку , а поскольку 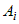 - некоторые числа, то и - некоторые числа, то и 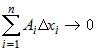 при при 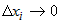 , , 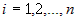 . . |
2) Если положить 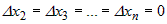 , то равенство (1) можно записать в виде , то равенство (1) можно записать в виде 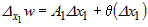 или или 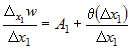 и перейти к пределу при и перейти к пределу при 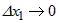 . Тогда . Тогда 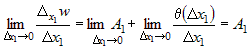 , откуда следует, что существует конечный предел , откуда следует, что существует конечный предел 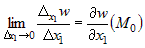 . Аналогично можно доказать существование конечных частных
производных . Аналогично можно доказать существование конечных частных
производных 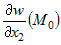 , , 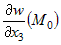 , :., , :., 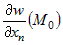 . . |
 Следствие 1. Следствие 1. |
Из доказательства теоремы следует, что числа 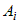 в определении дифференцируемой функции равны
значениям частных производных в точке дифференцируемости. Следовательно,
полное приращение функции в определении дифференцируемой функции равны
значениям частных производных в точке дифференцируемости. Следовательно,
полное приращение функции 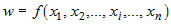 , дифференцируемой в точке , дифференцируемой в точке 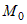 , можно представить в виде , можно представить в виде 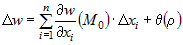 , где , где 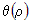 - бесконечно малая более высокого порядка, чем - бесконечно малая более высокого порядка, чем 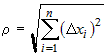 при всех при всех 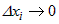 . . |
 Следствие 2. Следствие 2. |
Если у функции 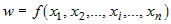 не существует конечная частная производная не существует конечная частная производная 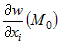 хотя бы по одной переменной хотя бы по одной переменной 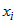 , то в точке , то в точке 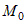 функция не является
дифференцируемой. функция не является
дифференцируемой. |
 Теорема 2. (Достаточное
условие дифференцируемости). Теорема 2. (Достаточное
условие дифференцируемости). |
|
Если функция 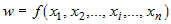 определена на множестве определена на множестве 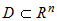 и имеет в точке и имеет в точке 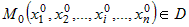 непрерывные частные производные по всем переменным непрерывные частные производные по всем переменным
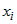 , то она в этой точке
дифференцируема. , то она в этой точке
дифференцируема. |
 Доказательство. Доказательство. |
|
При доказательстве ограничимся случаем функции
двух переменных. Для функции большего числа переменных доказательство
будет аналогичным.
Для функции 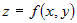 полное приращение в точке полное приращение в точке 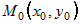 имеет вид: имеет вид: 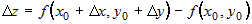 . Прибавим и вычтем в левой части этого соотношения
значение функции . Прибавим и вычтем в левой части этого соотношения
значение функции 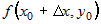 . Тогда . Тогда 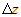 можно записать в следующем виде можно записать в следующем виде 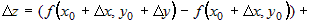
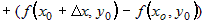 . .
Применяя теорему Лагранжа к разностям функций
одной переменной, стоящих в скобках, получим
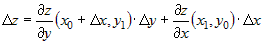 , (2), , (2), |
где 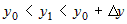 , , 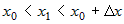 . Ясно, что при . Ясно, что при 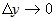 , , 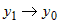 и при и при 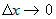 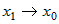 . .
Поскольку частные производные непрерывны, то
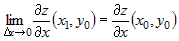
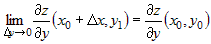 , ,
откуда следует, что 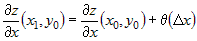 и и 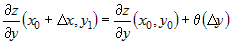 , где , где 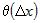 и и 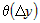 - бесконечно малые функции при - бесконечно малые функции при 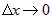 и и 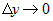 . Учитывая это, соотношение (2) можно
переписать в следующем виде . Учитывая это, соотношение (2) можно
переписать в следующем виде
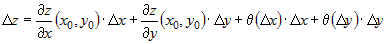 . .
Заметим, что выражение 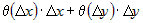 представляет собой бесконечно малую функцию при представляет собой бесконечно малую функцию при 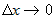 и и 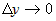 , имеющую более высокий порядок, чем , имеющую более высокий порядок, чем 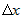 и и 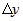 . Если обозначить эту бесконечно малую функцию . Если обозначить эту бесконечно малую функцию 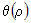 , где , где 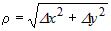 , то полное приращение функции запишется в виде: , то полное приращение функции запишется в виде: 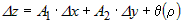 , где , где 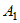 и и 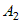 - вещественные числа, а - вещественные числа, а 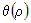 - бесконечно малая при - бесконечно малая при 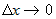 и и 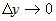 , более высокого порядка, чем , более высокого порядка, чем 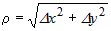 . Следовательно, функция . Следовательно, функция 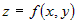 дифференцируема в точке дифференцируема в точке 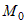 . . |
|
 |