 Теорема 1. Теорема 1. |
|
Пусть на множестве 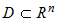 задана дифференцируемая по переменным задана дифференцируемая по переменным 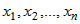 функция функция 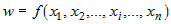 и функции и функции 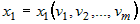 , , 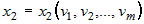 ,..:, ,..:, 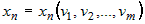 в свою очередь являются дифференцируемыми
функциями в свою очередь являются дифференцируемыми
функциями 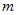 независимых переменных независимых переменных 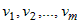 . Тогда функция . Тогда функция 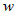 является сложной дифференцируемой функцией
независимых переменных является сложной дифференцируемой функцией
независимых переменных 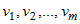 и частные производные от функции и частные производные от функции 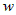 по этим переменным равны: по этим переменным равны:
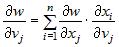 , где , где 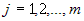 . . | |
 Доказательство. Доказательство. |
|
Из дифференцируемости функции 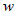 следует, что следует, что 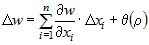 , где , где 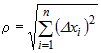 . Тогда . Тогда 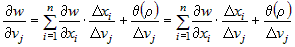 . .
В последнем равенстве перейдем к пределу при 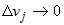 . Получим . Получим 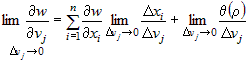 . .
Из дифференцируемости функций 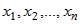 по переменным по переменным 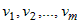 следует существование конечных пределов следует существование конечных пределов 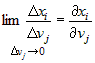 , а также непрерывность функций , а также непрерывность функций 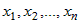 . Из непрерывности функций . Из непрерывности функций 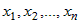 следует, что следует, что 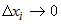 при при 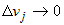 для всех для всех 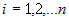 . При этом из дифференцируемости функций . При этом из дифференцируемости функций 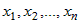 следует также, что следует также, что 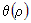 является бесконечно малой более высокого порядка,
чем является бесконечно малой более высокого порядка,
чем 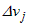 и, значит, и, значит, 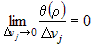 . Следовательно, . Следовательно, 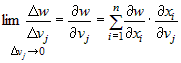 , при всех , при всех 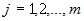 . Теорема
доказана. . Теорема
доказана. |
В частном случае, для сложной функции двух переменных 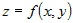 , где , где 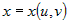 и и 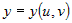 , частные производные по независимым переменным , частные производные по независимым переменным 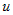 и и 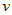 вычисляются по формулам вычисляются по формулам
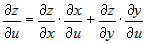 , ,
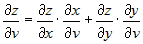 . . |
 Пример 1. Пример 1. |
|
Задана сложная функция 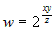 , где , где 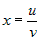 , , 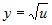 , , 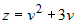 . Вычислить частные производные . Вычислить частные производные 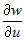 и и 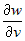 . . |
 Решение. Решение. |
|
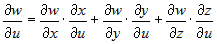 . .
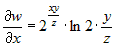 , , 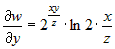 , , 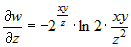 . .
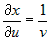 , , 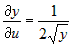 , , 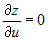 . .
Из этих соотношений следует, что
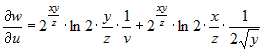 . .
Далее 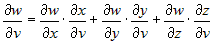 . .
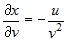 , , 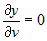 , , 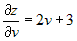 . .
Поэтому 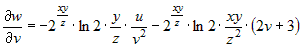 . . |
 Следствие 1. Следствие 1. |
Если на множестве 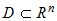 задана дифференцируемая по переменным задана дифференцируемая по переменным 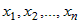 функция функция 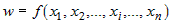 и если функции и если функции 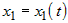 , , 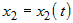 ,..:, ,..:,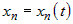 - дифференцируемые функции независимой
переменной - дифференцируемые функции независимой
переменной 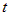 , то функция , то функция 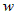 является сложной дифференцируемой функцией одной
переменной является сложной дифференцируемой функцией одной
переменной  и ее полная производная по независимой
переменной и ее полная производная по независимой
переменной 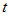 равна: равна: |
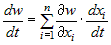 . . |
| Замечание. |
Иногда функция 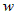 явно зависит от переменной явно зависит от переменной 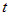 , то есть , то есть 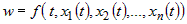 . В этом случае формула для полной
производной имеет вид: . В этом случае формула для полной
производной имеет вид: |
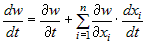 . . |
Здесь следует различать частную производную 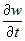 , которая вычисляется в предположении, что , которая вычисляется в предположении, что 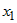 , , 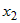 ,:, ,:,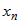 не зависят от переменной не зависят от переменной 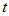 , и полную производную , и полную производную 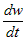 , которая учитывает и зависимость от , которая учитывает и зависимость от 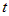 функций функций 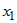 , , 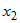 ,:, ,:,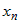 . . |
|
 |