|
Стационарные точки функции определяются из системы: 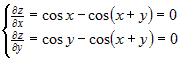 . Вычитая из первого уравнения второе, получим . Вычитая из первого уравнения второе, получим 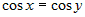 , или , или 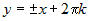 . Поскольку для заданной области . Поскольку для заданной области 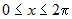 , то достаточно взять , то достаточно взять 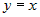 . Подставим это в первое уравнение. Получим . Подставим это в первое уравнение. Получим 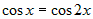 , откуда , откуда 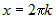 или или 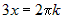 . Соотношение . Соотношение 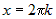 дает точки дает точки 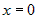 и и 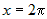 , лежащие на границе. Из соотношения , лежащие на границе. Из соотношения 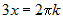 следует, что только одна стационарная точка следует, что только одна стационарная точка 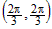 лежит внутри области (рис.10). Значение функции в
этой точке лежит внутри области (рис.10). Значение функции в
этой точке 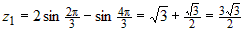 . .
Граница области задается уравнениями:
1. 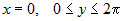 . На этой части границы . На этой части границы 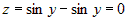 . .
2. 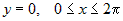 . На этой части границы . На этой части границы 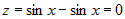 . .
3. 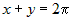 или или  , , 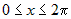 . На этой части границы . На этой части границы 
Следовательно, наибольшее значение функции равно 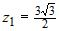 , а наименьшее , а наименьшее 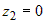 . . |