 Теорема 2. Теорема 2. |
|
Если 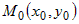 - стационарная точка дважды дифференцируемой функции - стационарная точка дважды дифференцируемой функции
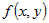 и если в некоторой окрестности этой точки и если в некоторой окрестности этой точки 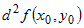 сохраняет знак, то функция в точке сохраняет знак, то функция в точке 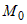 имеет экстремум. При этом если имеет экстремум. При этом если 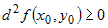 , то этот экстремум минимум. Если , то этот экстремум минимум. Если 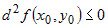 , то это максимум. , то это максимум. |
 Доказательство. Доказательство. |
|
Представим функцию 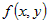 в точке в точке 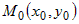 формулой Тейлора до членов второго порядка: формулой Тейлора до членов второго порядка: 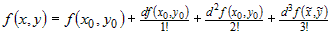 . С точностью до бесконечно малых более высокого
порядка, чем . С точностью до бесконечно малых более высокого
порядка, чем 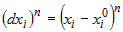 , учитывая, что в стационарной точке , учитывая, что в стационарной точке 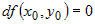 , формулу Тейлора можно записать в виде , формулу Тейлора можно записать в виде
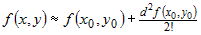 . .
Из последнего соотношения ясно, что если 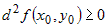 , то в некоторой окрестности , то в некоторой окрестности 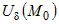 выполняется неравенство выполняется неравенство 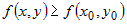 , что соответствует определению минимума. Если же , что соответствует определению минимума. Если же 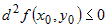 , то в некоторой окрестности , то в некоторой окрестности 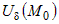 имеем неравенство имеем неравенство 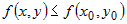 , из которого следует, что в точке , из которого следует, что в точке 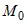 максимум. максимум. |
| Замечание. |
|
Если 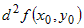 меняет знак в окрестности точки меняет знак в окрестности точки 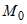 , то это еще не означает, что в этой точке нет
экстремума. , то это еще не означает, что в этой точке нет
экстремума. |
 Теорема 3. Теорема 3. |
|
Если 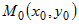 - стационарная точка дважды дифференцируемой функции - стационарная точка дважды дифференцируемой функции
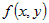 и если и если 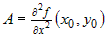 , , 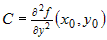 , , 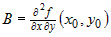 , то функция имеет экстремум, если , то функция имеет экстремум, если 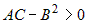 и не имеет экстремума, если и не имеет экстремума, если 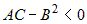 . При этом экстремум - максимум, если . При этом экстремум - максимум, если 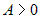 и минимум, если и минимум, если 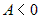 . . |
 Доказательство. Доказательство. |
|
В теореме 2 доказаны достаточные условия экстремума: если 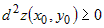 , то в точке , то в точке 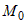 минимум; если минимум; если 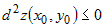 , то в точке , то в точке 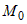 максимум. максимум.
Рассмотрим второй дифференциал в точке 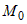 : : 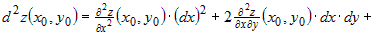
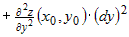 , или , или
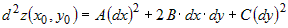 . .
Вынесем 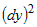 за скобку и обозначим за скобку и обозначим 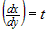 . Тогда . Тогда
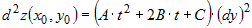 . .
Чтобы выражение 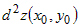 было определенного знака, дискриминант было определенного знака, дискриминант 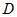 квадратного трехчлена квадратного трехчлена 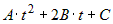 должен быть меньше или равен нулю. должен быть меньше или равен нулю. 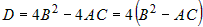 . Следовательно, при . Следовательно, при 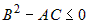 , или при , или при 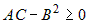 есть экстремум. При есть экстремум. При 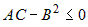 нет экстремума, при нет экстремума, при 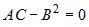 экстремум может быть, а может и не быть. Этот случай
требует дополнительных исследований. экстремум может быть, а может и не быть. Этот случай
требует дополнительных исследований.
Если 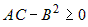 , то при , то при 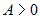 квадратный трехчлен квадратный трехчлен 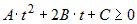 и экстремум является минимумом; при и экстремум является минимумом; при 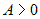 квадратный трехчлен квадратный трехчлен 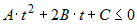 и экстремум является
максимумом. и экстремум является
максимумом. |
 Пример 2. Пример 2. |
|
Исследовать на экстремум функцию 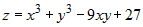 . . |
 Решение. Решение. |
|
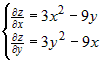 , , 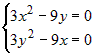 , , 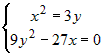 , , 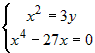 , , 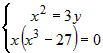 . Системе удовлетворяют две стационарные
точки . Системе удовлетворяют две стационарные
точки 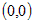 и и 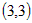 . .
Вычислим частные производные второго порядка 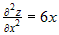 , , 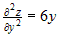 , , 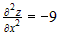 . Для первой стационарной точки . Для первой стационарной точки 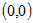 : : 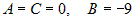 . Дискриминант . Дискриминант 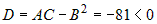 . Значит, в этой точке нет экстремума. Для точки . Значит, в этой точке нет экстремума. Для точки 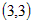 : : 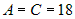 , , 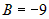 . Дискриминант . Дискриминант 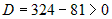 , а так как , а так как 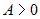 , то это точка
минимума. , то это точка
минимума. |
|
 |