 |
Основные
свойства определенного интеграла |
| 10.
|
Постоянный множитель можно выносить за знак
определенного интеграла, т.е. 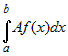 = =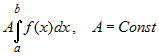 , если эти интегралы
существуют. , если эти интегралы
существуют. |
|
Действительно, 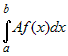 = =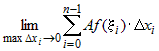 = =
=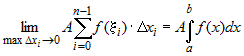 . . |
| 20.
|
Определенный интеграл от суммы нескольких
функций равен сумме интегралов от слагаемых, т.е.
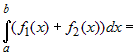 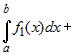 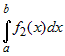
|
|
если 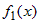 и и 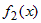 - интегрируемые на - интегрируемые на 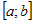 функции. функции. |
|
Так как 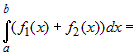 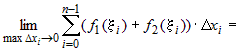
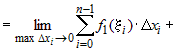 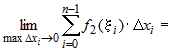 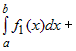 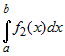 . .
|
| 30. |
Если на отрезке 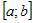 , где , где 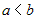 , интегрируемые функции , интегрируемые функции 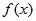 и и 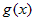 удовлетворяют условию удовлетворяют условию 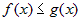 , то , то 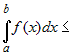 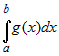 . . |
|
|
| 40. |
Если 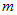 и и  - наименьшее и наибольшее значения
интегрируемой функции - наименьшее и наибольшее значения
интегрируемой функции 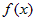 на отрезке на отрезке 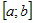 и и 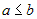 , то , то 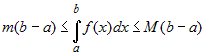 . . |
|
|
| 50. |
Теорема о
среднем. Если 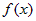 - непрерывна на отрезке - непрерывна на отрезке 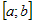 , то существует точка , то существует точка 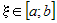 такая, что справедливо
равенство такая, что справедливо
равенство |
|
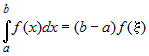 . . |
|
|
| 60.
|
Из определения определенного интеграла 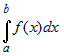 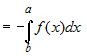 . . |
| 70. |
Для любых трех чисел 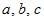 справедливо равенство справедливо равенство 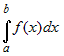 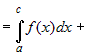 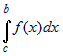 , если только все три интеграла
существуют. , если только все три интеграла
существуют. |
|
|
|
 |