|
1) Возьмем произвольную точку 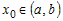 . Уравнение касательной к графику
функции в этой точке имеет вид: . Уравнение касательной к графику
функции в этой точке имеет вид:
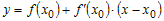 . .
Покажем, что в любой точке 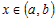 график функции расположен выше
этой касательной. график функции расположен выше
этой касательной.
Рассмотрим любую точку 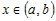 , удовлетворяющую условию , удовлетворяющую условию 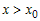 , и вычислим разность ординат функции , и вычислим разность ординат функции 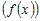 и касательной и касательной 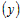 в этой точке: в этой точке:
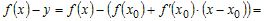
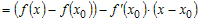 . .
Поскольку функция 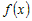 удовлетворяет условиям теоремы Лагранжа на
промежутке удовлетворяет условиям теоремы Лагранжа на
промежутке 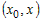 , то найдется точка , то найдется точка 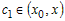 , для которой справедливо
равенство , для которой справедливо
равенство
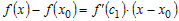 . .
Учитывая это, разность ординат функции и касательной в точке 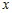 можно представить в виде можно представить в виде
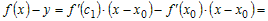
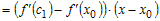 . .
Производная 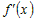 удовлетворяет условиям теоремы Лагранжа на
промежутке удовлетворяет условиям теоремы Лагранжа на
промежутке 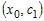 . Значит, найдется точка . Значит, найдется точка 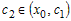 , для которой справедливо
равенство , для которой справедливо
равенство
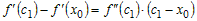 . .
Учитывая это, разность ординат функции и касательной в точке 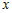 можно записать в виде можно записать в виде
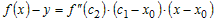 . .
Так как 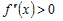 при всех при всех 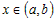 , а , а 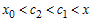 (рис.18), то (рис.18), то 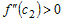 , , 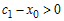 и и 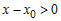 . Следовательно, . Следовательно, 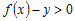 и график функции в точке и график функции в точке 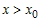 расположен выше
касательной. расположен выше
касательной.
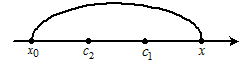 |
| Рис.
18 |
2) Рассмотрим любую точку 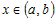 , удовлетворяющую условию , удовлетворяющую условию 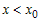 , и вычислим разность ординат функции , и вычислим разность ординат функции 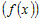 и касательной и касательной 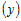 в этой точке: в этой точке:
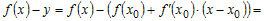
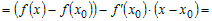
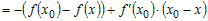 . .
Поскольку функция 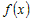 удовлетворяет условиям теоремы Лагранжа на
промежутке удовлетворяет условиям теоремы Лагранжа на
промежутке 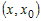 , то найдется точка , то найдется точка 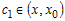 , для которой справедливо
равенство , для которой справедливо
равенство
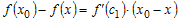 . .
Учитывая это, разность ординат функции и касательной в точке 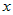 можно записать в виде можно записать в виде
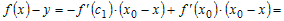
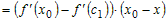 . .
Производная 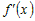 удовлетворяет условиям теоремы Лагранжа на
промежутке удовлетворяет условиям теоремы Лагранжа на
промежутке 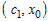 . Значит, найдется точка . Значит, найдется точка 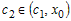 , для которой справедливо
равенство , для которой справедливо
равенство
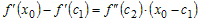 . .
Учитывая это, разность ординат функции и касательной в точке 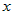 можно записать в виде можно записать в виде
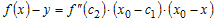 . .
Так как 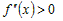 при всех при всех 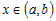 , а , а 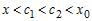 (рис. 19), то (рис. 19), то 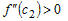 , , 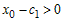 и и 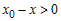 . Следовательно, . Следовательно, 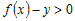 . Тогда график функции в точке . Тогда график функции в точке 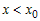 также расположен выше
касательной. также расположен выше
касательной.
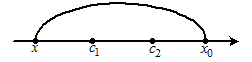 |
| Рис.
19. | |