 Параметрические уравнения
прямой Параметрические уравнения
прямой |
Прямая линия однозначно определена, если на ней задана
точка 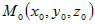 и ненулевой вектор, параллельный этой прямой. В
дальнейшем такой вектор будем называть направляющим вектором. Если и ненулевой вектор, параллельный этой прямой. В
дальнейшем такой вектор будем называть направляющим вектором. Если
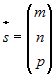 - направляющий вектор, то для любой точки - направляющий вектор, то для любой точки 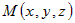 , принадлежащей прямой справедливо: , принадлежащей прямой справедливо: 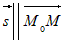 . Из определения коллинеарных векторов следует соотношение . Из определения коллинеарных векторов следует соотношение
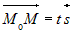 . Так как вектор . Так как вектор 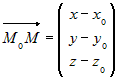 , то последнее равенство равносильно
системе , то последнее равенство равносильно
системе |
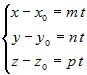 , или , или 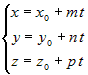 . . |
Полученные три уравнения называются параметрическими уравнениями прямой, а 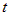 -
параметром. -
параметром. |
 Канонические уравнения
прямой Канонические уравнения
прямой |
| Если использовать условие коллинеарности векторов,
выраженное через их координаты, то получим уравнения, которые называются
каноническими
уравнениями прямой: |
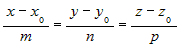 . . |
 Задача 1 Задача 1 |
|
Напишите канонические уравнения прямой, проходящей через точки 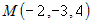 и и 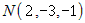 . . |
 Решение Решение |
|
Вектор 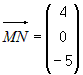 параллелен прямой, следовательно, мы можем выбрать
его в качестве направляющего вектора. Подставляя в канонические уравнения
прямой координаты любой из заданных точек, например параллелен прямой, следовательно, мы можем выбрать
его в качестве направляющего вектора. Подставляя в канонические уравнения
прямой координаты любой из заданных точек, например 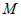 , получим систему канонических
уравнений прямой , получим систему канонических
уравнений прямой
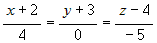 . .
|
Следует заметить, что канонические и параметрические
уравнения прямой выглядят различно, в зависимости от того, координаты какой
точки в них подставлены вместо чисел 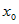 , 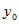 и 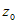 . Кроме того, в данной задаче одна из координат направляющего
вектора равна нулю, а это означает, что один из знаменателей в канонических
уравнениях равен нулю. Такая запись для канонических уравнений прямой считается
вполне допустимой. Чтобы понять, как в данном случае расположена в пространстве
прямая, перейдем к параметрическим уравнениям. Для этого каждое из трех равных
отношений обозначим через 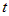 и получим 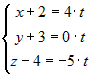 , или 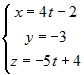 . Из последних уравнений ясно, что заданная прямая лежит в
плоскости 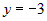 .
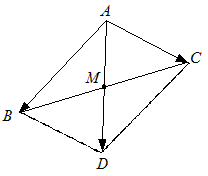 |
| Рис. 8 |
 Угол между прямыми Угол между прямыми |
Пусть 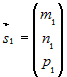 и и 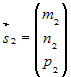 - направляющие векторы двух прямых. Угол - направляющие векторы двух прямых. Угол 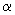 между прямыми определяется как
угол между их направляющими векторами. Для косинуса этого угла справедлива
формула: между прямыми определяется как
угол между их направляющими векторами. Для косинуса этого угла справедлива
формула: |
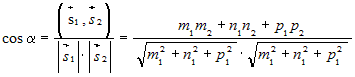 . . |
 Условие
перпендикулярности прямых Условие
перпендикулярности прямых |
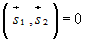 или или 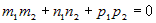 . . |
 Условие параллельности
прямых Условие параллельности
прямых |
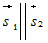 или или 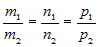 . . |
 Условия пересечения
прямых в пространстве Условия пересечения
прямых в пространстве |
Если 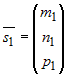 и и 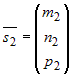 - направляющие векторы двух прямых, а - направляющие векторы двух прямых, а 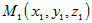 и и 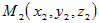 - точки на этих прямых, то прямые пересекаются или
скрещиваются в зависимости от того, компланарны или нет векторы - точки на этих прямых, то прямые пересекаются или
скрещиваются в зависимости от того, компланарны или нет векторы 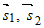 и и 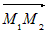 (рис.9). (рис.9). |
Прямые скрещиваются, если смешанное произведение 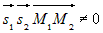 (рис.9 a). (рис.9 a). |
Прямые пересекаются, если смешанное произведение 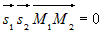 (рис.9 b). (рис.9 b). |
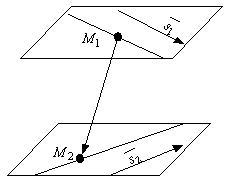 |
| Рис. 9
a | |
|
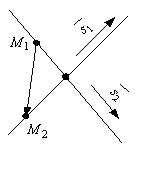 |
| Рис. 9
b | | |
 Приведение общих уравнений прямой к
каноническому виду Приведение общих уравнений прямой к
каноническому виду |
Пусть прямая задана общими уравнениями 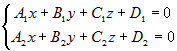 . . |
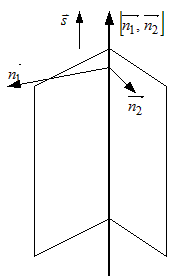 |
| Рис. 10 | |
Если нужно привести ее уравнения к каноническим или
параметрическим, то следует выбрать на этой прямой какую-то точку и найти
вектор, параллельный ей. Координатами точки, принадлежащей прямой,
является любое из решений заданной линейной системы. Направляющим вектором
прямой является вектор 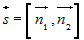 , где , где 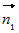 и и 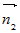 - нормальные векторы плоскостей, задающих прямую
(рис. 10). - нормальные векторы плоскостей, задающих прямую
(рис. 10). |
|
 |