 |
Следствия: |
| 1). |
Произведение конечного числа
бесконечно малых функций есть б.м. в той же точке. Действительно б.м.
функция является ограниченной, т. к. имеет конечный предел. |
| 2). |
Произведение конечного числа бесконечно больших функций есть
б.б. в той же точке. Действительно, если 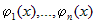 - б.б., то - б.б., то |
|
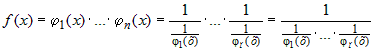 , , |
|
откуда следует, что функции 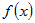 представляет собой представляет собой 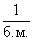 , то есть б.б. , то есть б.б. |
Сформулируем еще два свойства для бесконечно больших функций:
Сумма
конечного числа функций, б. б. в одной точке, и имеющих одинаковый знак,
является б.б. того же знака в той же точке.
Сумма функции, б.б. в точке 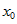 , и ограниченной функцию в
окрестности точке , и ограниченной функцию в
окрестности точке 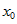 есть б.б. функция в той же точке. есть б.б. функция в той же точке.
|
 |