Пусть функция 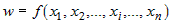 имеет частные производные в точке имеет частные производные в точке 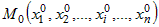 из ее области определения из ее области определения 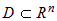 . Будем называть их частными производными первого порядка. Так
как они являются функциями тех же переменных, что и данная функция, то у каждой
из них могут существовать частные производные по любому из этих
аргументов. . Будем называть их частными производными первого порядка. Так
как они являются функциями тех же переменных, что и данная функция, то у каждой
из них могут существовать частные производные по любому из этих
аргументов.
Полученные таким образом частные производные называются
частными производными второго
порядка.
В частности для функции
двух переменных 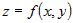 можно составить четыре частных производных второго
порядка, которые обозначаются следующим образом: можно составить четыре частных производных второго
порядка, которые обозначаются следующим образом:
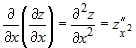 ; ; 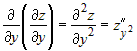 ; ; 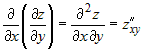 ; ; 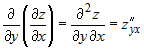 . .
Вообще для каждой из этих частных производных второго
порядка можно дать и строгое определение.
В частности, для функции двух переменных 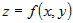 , учитывая независимость частных производных от порядка
дифференцирования, справедливо: , учитывая независимость частных производных от порядка
дифференцирования, справедливо:
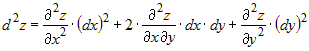 . . | Аналогично определяются дифференциалы
более высокого порядка. Дифференциал третьего порядка или третий дифференциал
- это дифференциал от второго дифференциала.
Легко показать, что для
функции двух переменных 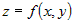 формула для третьего дифференциала имеет вид: формула для третьего дифференциала имеет вид:
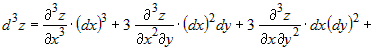
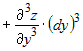 . . |
Формулы для второго дифференциала
функции двух переменных 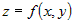 удобно записывать в символическом виде: удобно записывать в символическом виде:
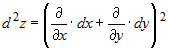 , , | где под записью 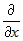 понимается операция взятия частной производной по понимается операция взятия частной производной по 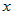 , а под записью , а под записью 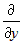 понимается операция взятия частной производной по понимается операция взятия частной производной по 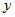 . .
В общем случае для дифференциала 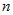 - го порядка функции двух переменных - го порядка функции двух переменных 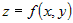 справедлива формула: справедлива формула:
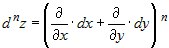 . . |
| Замечание 2. |
|
Сравнивая формулы для дифференциала второго порядка в случае, когда
что 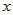 и и 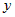 - независимые переменные, и когда они в свою очередь
являются функциями двух переменных, можно сделать вывод, что второй
дифференциал не обладает свойством инвариантности. - независимые переменные, и когда они в свою очередь
являются функциями двух переменных, можно сделать вывод, что второй
дифференциал не обладает свойством инвариантности. |
 Пример 2. Пример 2. |
|
Вычислите 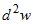 , если , если 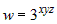 . . |
 Решение. Решение. |
|
В разделе 6.3.1 был вычислен 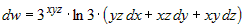 . Тогда . Тогда
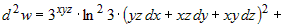
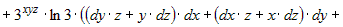
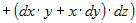 . Упрощая полученное выражение, запишем . Упрощая полученное выражение, запишем
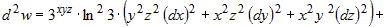
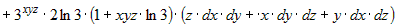 . .
|
|
 |