 |
Вычисление
площадей |
| 1. |
Если 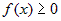 на на 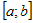 , то площадь криволинейной трапеции, ограниченной
кривой , то площадь криволинейной трапеции, ограниченной
кривой 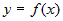 , осью , осью 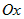 и прямыми и прямыми 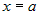 и и 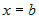 (рис. 6), равна: (рис. 6), равна:
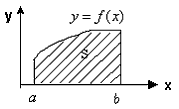 |
| Рис.
6 |
|
| 2. |
Если 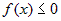 на на 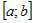 , то определенный интеграл , то определенный интеграл 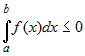 и по абсолютной величине равен площади
криволинейной трапеции и по абсолютной величине равен площади
криволинейной трапеции 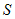 (рис. 7), т.е. (рис. 7), т.е.
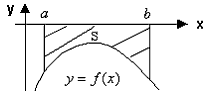 |
| Рис.
7 | |
| 3. |
Если 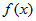 конечное число раз меняет свой знак на отрезке конечное число раз меняет свой знак на отрезке 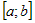 , то интеграл по всему отрезку , то интеграл по всему отрезку 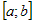 разбиваем на сумму
интегралов по частичным отрезкам (рис. 8), или разбиваем на сумму
интегралов по частичным отрезкам (рис. 8), или
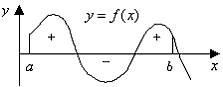 |
| Рис. 8 |
|
| 4. |
Если кривая задана уравнениями в параметрической форме (рис.10): 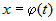 и и 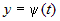 , где , где 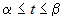 и и 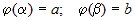 . .
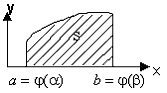 |
| Рис. 10 |
Тогда площадь криволинейной трапеции будет
определяться, как :
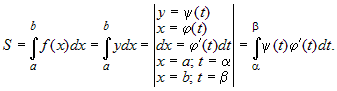 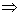
|
| 5. |
Площадь сектора в полярных координатах
Пусть кривая задана уравнением: 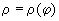 , где , где 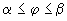 . .
 |
| Рис.
10 |
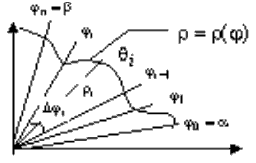
Разобьем площадь
криволинейного сектора на 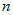 частей лучами: частей лучами: 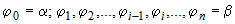 (рис. 11). В каждом частном угле (рис. 11). В каждом частном угле 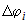 возьмем луч возьмем луч 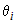 и найдем и найдем 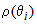 . Тогда площадь криволинейного сектора будет равна . Тогда площадь криволинейного сектора будет равна 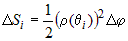 . Следовательно, площадь всего «ступенчатого» сектора
будет равна . Следовательно, площадь всего «ступенчатого» сектора
будет равна 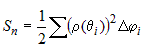 . Получили интегральную сумму . Получили интегральную сумму 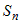 . При переходе к пределу при . При переходе к пределу при 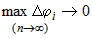 , получим, что , получим, что 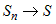 . По определению определенного интеграла площадь сектора равна . По определению определенного интеграла площадь сектора равна
|
|
 Вычисление объема тела по
площадям параллельных сечений Вычисление объема тела по
площадям параллельных сечений
|
|
Пусть 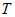 - некоторое тело, расположенное вдоль оси - некоторое тело, расположенное вдоль оси 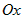 . Предположим, что для любого . Предположим, что для любого 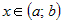 известна известна 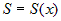 - площадь любого сечения этого тела плоскостью,
перпендикулярной оси - площадь любого сечения этого тела плоскостью,
перпендикулярной оси 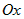 (рис. 13). (рис. 13).
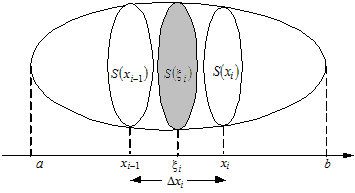 |
| Рис.
13. |
Предположим, что 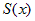 есть непрерывная функция от есть непрерывная функция от 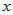 . Проведем плоскости . Проведем плоскости 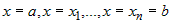 . Эти плоскости разобьют тело . Эти плоскости разобьют тело 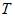 на на 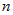 слоев. слоев.
В каждом частичном промежутке 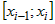 возьмем произвольную точку возьмем произвольную точку 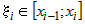 и построим цилиндрическое тело, образующая которого
параллельна оси и построим цилиндрическое тело, образующая которого
параллельна оси 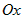 , а направляющая представляет собой контур сечения тела , а направляющая представляет собой контур сечения тела
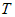 плоскостью плоскостью 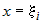 . .
Объем такого цилиндра равен 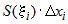 , где , где 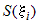 -площадь основания цилиндра, -площадь основания цилиндра, 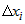 - его высота. Сумма объемов всех цилиндров равна - его высота. Сумма объемов всех цилиндров равна 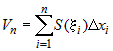 . .
Т.к. 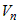 представляет собой интегральную сумму для
непрерывной функции представляет собой интегральную сумму для
непрерывной функции 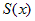 на отрезке на отрезке 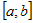 , то можно доказать, что существует ее
предел, который по определению является определенным интегралом. , то можно доказать, что существует ее
предел, который по определению является определенным интегралом.
|
| Длина дуги в декартовых
координатах |
 Пример. Пример. |
|
Найдем длину кардиоиды 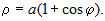 (рис. 16). (рис. 16).
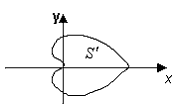 |
| Рис. 16 |
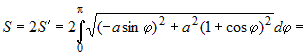
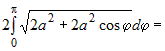
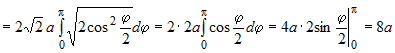
|
|
 |