|
Напомним, что функция двух переменных 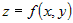 задает в пространстве с введенной декартовой
системой координат некоторую поверхность. задает в пространстве с введенной декартовой
системой координат некоторую поверхность.
Уравнение плоскости, проходящей через точку 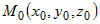 , имеет вид: , имеет вид: 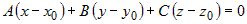 . Если . Если 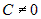 , то можно разрешить это уравнение относительно переменной , то можно разрешить это уравнение относительно переменной
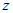 , тогда получим уравнение , тогда получим уравнение 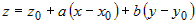 , где , где 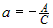 , , 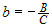 . .
Выясним, при каких значениях параметров 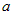 и и 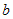 это уравнение является уравнением касательной
плоскости к поверхности это уравнение является уравнением касательной
плоскости к поверхности 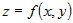 в точке в точке 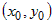 . .
Положив в этом уравнении 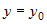 , получим уравнение прямой , получим уравнение прямой 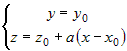 , которая при , которая при 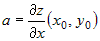 является уравнением касательной к кривой является уравнением касательной к кривой 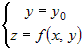 в точке в точке 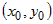 . .
Положив в этом уравнении 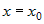 , получим уравнение прямой , получим уравнение прямой
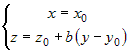 , которая при , которая при 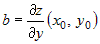 является уравнением касательной к кривой является уравнением касательной к кривой 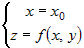 в точке в точке 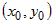 . .
Ясно, что обе эти касательные прямые принадлежат искомой касательной
плоскости (рис.9). Поскольку через две пересекающиеся прямее можно
провести только одну плоскость, то уравнение 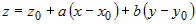 является уравнением касательной плоскости к
поверхности является уравнением касательной плоскости к
поверхности 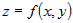 в точке в точке 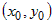 при при 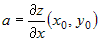 и и 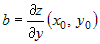 . .
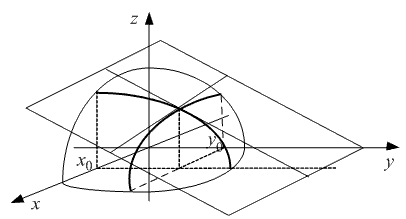 |
| Рис.9. | |