 Несобственные
интегралы Несобственные
интегралы |
|
В определении интеграла 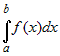 предполагалось, что: предполагалось, что:
1) промежуток интегрирования 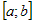 конечен. конечен.
2) функция 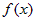 определена и непрерывна на определена и непрерывна на 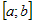 . .
Такой определенный интеграл называется собственным (слово собственный обычно
опускается).
Если нарушается хотя бы одно из условий 1) или 2), то интеграл
называется несобственным определенным
интегралом.
Выясним смысл этого нового понятия для двух
простейших случаев. |
| Несобственный интеграл с бесконечным пределом
интегрирования |
|
 Несобственный интеграл с
бесконечным пределом интегрирования Несобственный интеграл с
бесконечным пределом интегрирования
|
|
Этот интеграл по определению равен 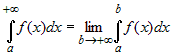 .
Несобственный интеграл с бесконечным пределом интегрирования часто
называют несобственным интегралом 1 рода. .
Несобственный интеграл с бесконечным пределом интегрирования часто
называют несобственным интегралом 1 рода.
Если предел существует и конечен, то интеграл называется
сходящимся, в противном случае интеграл называется
расходящимся.
Если 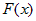 -
первообразная функция для подынтегральной функции -
первообразная функция для подынтегральной функции 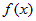 , то , то
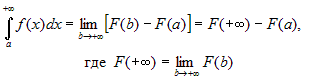
Аналогичным образом определяются интегралы: 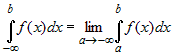 и и 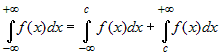 . . |
 Пример. Пример. |
|
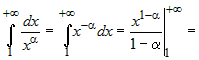 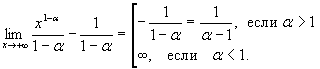 . .
Если 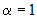 , то , то 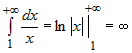 . Следовательно, . Следовательно,
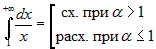
Во многих случаях достаточно установить, сходится
данный интеграл или расходится. Для этого могут быть полезными следующие
теоремы. |
| Несобственный интеграл от разрывной
функции |
|
 Несобственный интеграл от
разрывной функции Несобственный интеграл от
разрывной функции
|
|
Пусть 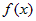 непрерывна при непрерывна при 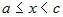 и имеет точку бесконечного разрыва при и имеет точку бесконечного разрыва при 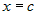 . Тогда несобственный интеграл . Тогда несобственный интеграл
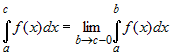
называется сходящимся или
расходящимся в зависимости от того,
существует или нет конечный предел.
Аналогично определяются интегралы:
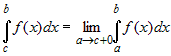 (бесконечный разрыв в точке (бесконечный разрыв в точке 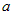 ) )
и 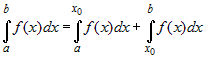 (бесконечный разрыв в точке (бесконечный разрыв в точке 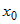 ). ). |
 Пример. Пример. |
|
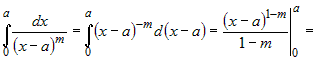
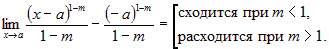
Если 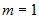 , то , то 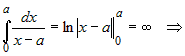 расходится. расходится.
Таким образом 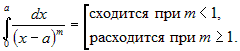
Рассмотрим теоремы, устанавливающие признаки
сходимости несобственных интегралов от разрывной
функции. |
|
 |