 Производная произведения
функций Производная произведения
функций |
Если функции 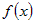 и и 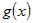 дифференцируемы в точке дифференцируемы в точке 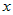 , то функция , то функция 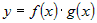 тоже дифференцируема в точке тоже дифференцируема в точке 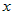 и ее производная вычисляется по
правилу: и ее производная вычисляется по
правилу: |
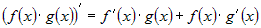 . . |
 Доказательство Доказательство |
|
Составим приращение 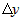 для функции для функции 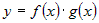 . .
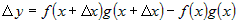 . .
Прибавим и вычтем выражение 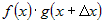 и сгруппируем слагаемые
попарно. и сгруппируем слагаемые
попарно.
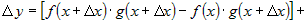
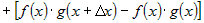 . .
Из первой скобки можно вынести общий множитель 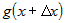 , а из второй - , а из второй - 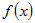 . .
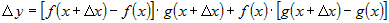 . .
Выражения в скобках представляют собой приращения функций 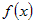 и и 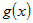 , поэтому , поэтому
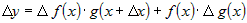 . .
Тогда, используя определение производной, можно
записать:
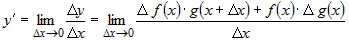 , или , или
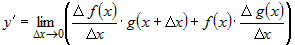 . .
Используя теоремы о пределе суммы и произведения
функций, получим:
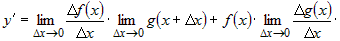 . .
Из дифференцируемости функции 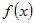 следует, что существует конечный предел следует, что существует конечный предел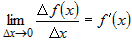 . .
Из дифференцируемости функции 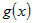 следует, что существует конечный предел следует, что существует конечный предел 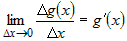 . .
Так как дифференцируемая в точке 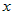 функция функция 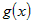 непрерывна в этой точке, то по определению
непрерывной функции непрерывна в этой точке, то по определению
непрерывной функции 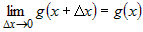 . Следовательно, . Следовательно,
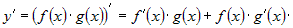
|
 Следствие Следствие |
|
Если функция 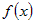 дифференцируема в точке дифференцируема в точке 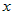 , а , а 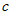 - конечное число, то функция - конечное число, то функция 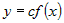 тоже дифференцируема в точке тоже дифференцируема в точке 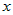 и при этом и при этом
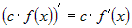 . .
|
 Доказательство Доказательство |
|
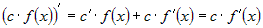 . .
|
 Производная частного Производная частного |
Если функции 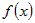 и и 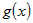 дифференцируемы в точке дифференцируемы в точке 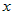 и и 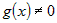 , то функция , то функция 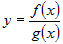 тоже дифференцируема в точке тоже дифференцируема в точке 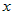 и ее производная вычисляется по
правилу: и ее производная вычисляется по
правилу: |
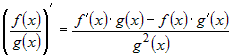 . . |
 Доказательство Доказательство |
|
Составим приращение 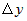 для функции для функции 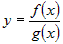 . .
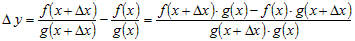 . .
Прибавим и вычтем в числителе выражение 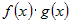 и сгруппируем слагаемые попарно.
Получим и сгруппируем слагаемые попарно.
Получим
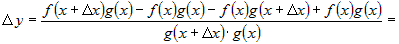 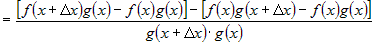 . .
Из первой скобки можно вынести общий множитель 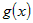 , а из второй - , а из второй - 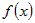 . Тогда приращение . Тогда приращение 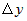 запишется в виде: запишется в виде:
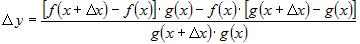 , или , или
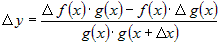 . .
Используя определение, запишем выражение для
производной в виде
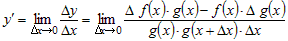 , ,
затем, проведя под знаком предела тождественные преобразования и
учитывая, что 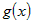 не зависит от переменной не зависит от переменной 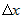 , преобразуем его , преобразуем его
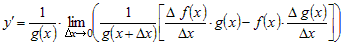 . .
Так как 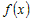 и и 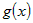 не зависят от переменной не зависят от переменной 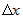 , то по теоремам о пределах получим , то по теоремам о пределах получим
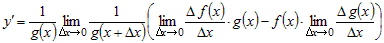 . .
Из дифференцируемости 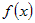 следует, что существует конечный предел следует, что существует конечный предел 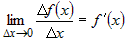 . Из дифференцируемости (и непрерывности) . Из дифференцируемости (и непрерывности) 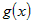 следует, что существуют конечные пределы следует, что существуют конечные пределы 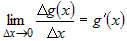 и и 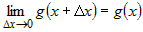 . Поэтому . Поэтому
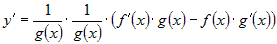 , ,
или
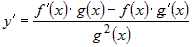 . . |
 Теорема о производной
обратной функции Теорема о производной
обратной функции |
Если функция 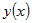 монотонна на промежутке монотонна на промежутке 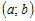 и дифференцируема
в точке и дифференцируема
в точке 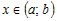 , то
существует обратная функция , то
существует обратная функция 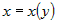 , которая дифференцируема в точке , которая дифференцируема в точке 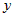 и ее
производная определяется из соотношения и ее
производная определяется из соотношения |
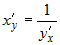 . . |
 Доказательство Доказательство |
|
Функция 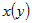 дифференцируема в точке дифференцируема в точке 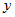 , если существует конечный
предел , если существует конечный
предел
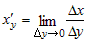 . .
Докажем это. Поскольку по условию существует конечный предел 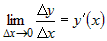 , причем в силу
монотонности , причем в силу
монотонности 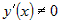 , то
по теореме о пределе частного существует и конечен предел , то
по теореме о пределе частного существует и конечен предел 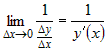 . .
Из дифференцируемости функции 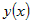 в точке в точке 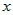 следует ее непрерывность в этой точке, а это
означает, что при следует ее непрерывность в этой точке, а это
означает, что при 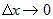 приращение функции приращение функции 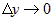 . Учитывая это, можно от
предела при . Учитывая это, можно от
предела при 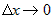 перейти к пределу при перейти к пределу при 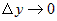 . Тогда . Тогда
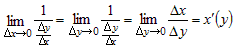 . .
Следовательно, существует конечная производная 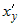 , которая вычисляется по
правилу: , которая вычисляется по
правилу:
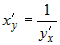 . .
|
 Производная сложной функции Производная сложной функции |
Если функция 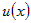 дифференцируема в точке дифференцируема в точке 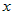 и функция и функция 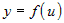 дифференцируема в точке дифференцируема в точке 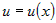 , то суперпозиция функций (сложная функция) , то суперпозиция функций (сложная функция) 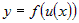 дифференцируема в точке дифференцируема в точке 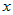 и ее производная по переменной и ее производная по переменной 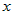 вычисляется по правилу: вычисляется по правилу: |
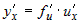 . . |
| при этом нижние индексы показывают, по какой переменной
берется производная. |
 Доказательство Доказательство |
|
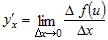 . .
Умножим числитель и знаменатель дроби под знаком предела на приращение
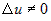 , получим , получим
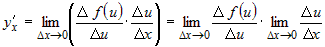 . .
Так как функция 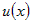 дифференцируема точке дифференцируема точке 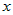 , следовательно, она в этой точке непрерывна. Поэтому
приращение функции , следовательно, она в этой точке непрерывна. Поэтому
приращение функции 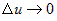 при при 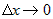 . Переходя в первом сомножителе от предела при . Переходя в первом сомножителе от предела при 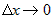 к пределу при к пределу при 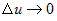 , получим , получим
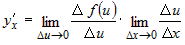 . .
Из дифференцируемости функций 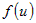 и и 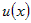 следует, что оба предела существуют, конечны и равны
производным по переменным следует, что оба предела существуют, конечны и равны
производным по переменным 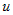 и и 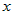 соответственно, то есть соответственно, то есть 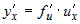 . . |
| Замечание |
|
Правило дифференцирования суперпозиции функций (сложной функции)
следует понимать так, что если требуется вычислить производную от функции
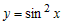 , то следует иметь в виду, что вычисляется производная
суперпозиции функций , то следует иметь в виду, что вычисляется производная
суперпозиции функций 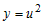 , где , где 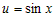 . Тогда следует вычислить производную . Тогда следует вычислить производную  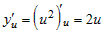 и производную и производную 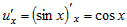 . Далее по правилу дифференцирования сложной функции . Далее по правилу дифференцирования сложной функции
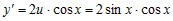 . .
|
|
 |