|
Пусть 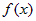 - непрерывна на - непрерывна на 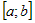 . Рассмотрим интеграл . Рассмотрим интеграл 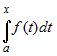 , где , где 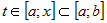 (во избежание путаницы,
переменная интегрирования обозначена другой буквой). (во избежание путаницы,
переменная интегрирования обозначена другой буквой).
При постоянном a этот интеграл будет представлять собой функцию
верхнего предела x. Эту функцию мы обозначим через 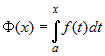 . .
Если 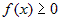 , то величина , то величина 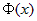 численно равна площади криволинейной трапеции численно равна площади криволинейной трапеции 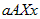 (рис. 4). Очевидно, что площадь изменяется в
зависимости от x. (рис. 4). Очевидно, что площадь изменяется в
зависимости от x.
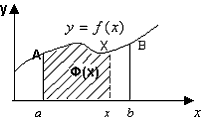 |
| Рис.
4. | |